050

A HibUl. IM1U.1 ,Vv»«    r ), buui :uO

ISBN D4H1II f-\ © l>. »N TOS >«}

50

3 ELEKTRONOWA STRUKTURA ATOMU

Podstawę do przypisania fotonowi określonej nuisy daje teoria względności Einsteina. Wiadomo już z poprzedniego rozdziału, że wskazuje ona na możliwość zamiany energii w masę i odwrotnie. Korzystając z równania (2.1). możemy więc przypisać fotonowi masę równoważną jego energii e:    _f

»i = —    (3.6)

a po wprowadzeniu zależności (3.2) uzyskujemy

(3.7)

hv h ^m c³    cA

e _ hv _ h ~^m< ~ c² ~ c A

przy czym c oznacza prędkość światła. A — długość fali. odpowiadającą promieniowaniu zawierającemu kwanty f. = hv. Uwzględniając równanie (3.7). znajdujemy, że pęd fotonu o masie m i prędkości c wynosi

r    h \i    h

(3.8)

Zgodność zjawiska Comptona z prawem zachowania pędu polega na tym. że suma wektora pędu fotonu wtórnego |>; — hv. je oraz wektora pędu elektronu p_c — m.v równa się wektorowi pędu fotonu padającego p, = liv,/c. Dvxlawanic tych wektorów przedstawiono na rys. 3.3. Zmiana długości wektorów pj i p, (a więc i zmiana energii fotonu wtórnego i elektronu) przy zachowaniu stałej długości wektora p, (a więc stałej energii fotonu pierwotnego) musi spowodować zmianę kąta er pomiędzy wektorami p i p_c. a zarazem kąta. pod jakim rozbiegają się foton wtórny i elektron.

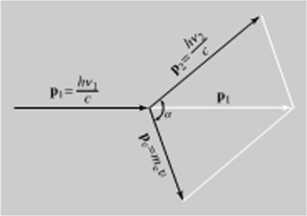
Rys. 3.1 Efekt Comptona Iobjaśnienia w tekście)

Wykrycie zjawiska Comptona ugruntowało ostatecznie teorię kwantową światła. Nie oznacza to bynajmniej, że teoria falowa straciła swoje znaczenie. Wprawdzie zjawisk, które można wyjaśnić za pomocą leorii kwantowej — a są to zjawiska związane z emisją i pochłanianiem światła — nie wyjaśnia teoria falowa, ale też zjawisk, które wyjaśnia teoria falowa — są to zjawiska związane z rozchodzeniem się światła — nic można zrozumieć wyłącznie na gruncie teorii kwantowej. Każda z tych teorii stosuje się do innego rodzaju zjawisk. Światło zatem zachowuje się tak. jak gdyby miało naturę zarówno falową, jak i korpuskulatną,