059

A HibUl. IM1U.1 .Vv»«    r ), buui :uO

ISBN D4H1II ł-7. © l>. »N TOS >«}

59

3 4 ATOM WOOOftU

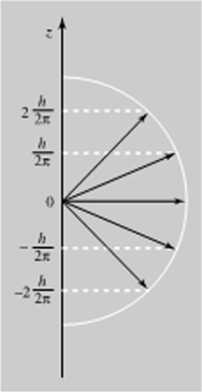
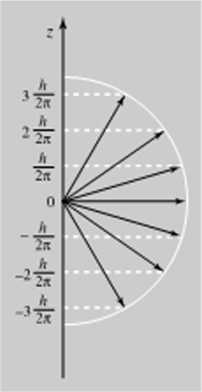
Rw. 3.6. Kwantowanie przestrzenne mimieniu    Rys. 3.7. Kwantowanie przestrzenne momentu

pęiłu cieku vmi w aliraue wodoru (/ = 2)    pędu elektronu w utomic wodoru (/ = 3)

w którym m oznacza magnetyczną liczby kwantową przyjmującą wartości liczb całkowitych ud —I do +/•

-I <111 <1

Twierdzenie, że składowa zetowa momentu pędu może przyjmować tylko niektóre wartości, jest równoznaczne z twierdzeniem, że sam wektor momentu pędu może przyjmować tylko niektóre położenia w stosunku do osi Rozważmy przypadek, w którym I = 1 i \f = _V'7</ + 1 )£ = %/2^f. Magnetyczna liczba kwantowa może wówczas przyjąć 3 różne wartości:    1.0 oraz I. którym odpowiadają wartości składowej M wy

noszące: —A/2rt,0 oraz lt/2n i wyznaczające 3 różne położenia wektora przedstawione na rys. 3.5.

Gdy 1 = 2, istnieje 5 możliwych wartości magnetycznej liczby kwantowej: -2. -1.0. I i 2. Wektor momentu pędu M - </2< 2 + 1) ~ = v' 6^j może wtedy przyjąć 5 różnych położeń w stosunku do kierunku wyróżnionego w przestrzeni (rys. 3.6). Gdy / = 3 i ni = -3. -2. —1.0. 1.2.3. wektor momentu pędu M = _v‘‘3(3 -ł- 1= v'12^j może być nachylony pod siedmioma różnymi kątami w stosunku do kierunku wyróżnionego (rys. 3.7) itd.

7. powyższych rozważań wynika, żc trzy wielkości, jakie udaje się dla atomu w\>doru obliczyć w toku rozwiązywania równania Schródingera: energia całkow ita elektronu. £. jego moment pędu. A#, oraz składowa zetowa momentu pędu. A/., mogą przyjmować tylko niektóre wartości, a mianowicie wartości wyznaczone przez odpowiednie liczby kwantowe. Ten stan rzeczy określa się mów iąc, ze E. M oraz M. ulegają kwantowaniu.