0042

44

VIII. Funkcja pierwotna (całka nieoznaczona)

Niech teraz m< — 1, a więc m = —/i, /u>l. Zastosujemy tym razem wzór (II)

, (1 -_zyi*z<»+i>i2    , m + 2 _r

^Z -1^-i--¹---•'-1/2,1

m+1    /rc+1

(m + D/2 i

skąd

_ —    ^łVl—x² | —2

H-

(11-2) ■

Za pomocą tego wzoru możemy zmniejszać wartość fi o 2 i stopniowo sprowadzić obliczenia albo do

*w-

f/jc

= i„ I-¹-)⁷¹--¹

+ C

dla fi nieparzystego, albo do

H- 2 =

r

+ c

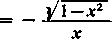
dla ju parzystego.

2) Jeśli do całki (*)

Jn + l = J (_x2_+a2y + l ⁼ Y J ⁱ"*°2-'^l2dz = /-(„ + !),-1/2    (« = 1, 2, 3, ...)

zastosować wzór (I):

2/i-l

2/i

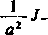
-1/2 .

,    (o² + z)-"z^1/2 ,

•»-(n+l).-l/2-r---T

to powracając do /„ otrzymamy znany nam już [271, (6)] wzór redukcyjny

_T _    1    _x__i 2n—l 1 _r

"⁺¹    2/ia²    (jc² + o²)"    2n a² "

281. Całkowanie wyrażeń postaci R(x, \/ax²+bx+c). Podstawienia Eulera. Przechodzimy do rozpatrzenia bardzo ważnej klasy całek

(4)    j R(x,\/ax² + bx+ć) dx .

Zakładamy oczywiście, że trójmian kwadratowy nie ma pierwiastków równych, a więc że jego pierwiastek kwadratowy nie może być zastąpiony wyrażeniem wymiernym. Zapoznamy się z trzema podstawieniami, zwanymi podstawieniami Eulera, za pomocą których można zawsze sprowadzić do postaci wymiernej wyrażenie podcałkowe.

Pierwsze podstawienie może być zastosowane w przypadku, gdy a > 0. Przyjmujemy wówczas

}/ax² + óx+c = t—j/ax(²) .

(¹)    Analogicznie można też badać całkę

f dx

J (x¹—a²y^+l '

(²)    Można przyjąć również J/ax²+bx+c = t+]/ax.