0026

28

VIII. Funkcja pierwotna (całka nieoznaczona)

Zastosujemy teraz podstawienie

x+-y = t, dx = dt,

x² + px + q = t² + a², Mx+N = Mt +

W przypadku III otrzymujemy

/

Mx+N

dx

f

Mt+(N—y Mp)

t² + a²

. M f 2t di ( Mp \ r dt

* ~ t J F+?- + ("- -r)J s? -

x* + px + q

= ~ In (t²+a²)+ —(N— ^ arc tgi_ +C ^2    a \    2 ) a

lub wracając do x i podstawiając zamiast a jego wartość

h

Mx + N + px + q

dx = 4r-ln {x² + px+q)+

2 N-Mp l/4 q~P²

arc tg

2 x+p l/4 q — p^z

+ C.

W przypadku IV to samo podstawienie daje

(1) f    ^{Mx + N}    j_::    f «>+<"-

J (x² + px + q)^m    J (r² + fl²)"

M r 2t dt / Mp\r dt

2 J (»²+fl²r    2    (f²+a²r

Pierwsza całka po prawej stronie równości może być łatwo obliczona przez podstawienie t²+a² — u, 21 dt = du

(2)

/

21 dt

(t²+a²)^m

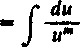
1

m — 1

1

u"*¹

1

m-1

+ C.

Natomiast druga po prawej stronie przy dowolnym m może być obliczona ze wzoru redukcyjnego (6) 271. Pozostaje więc tylko podstawić z powrotem w wyniku t =    ,

aby powrócić do zmiennej x.

Tym wyczerpuje się zagadnienie całkowania ułamków prostych.

274. Rozkład ułamków właściwych na ułamki proste. Zatrzymamy się teraz na pewnym twierdzeniu z-algebry, które ma jednak zasadnicze znaczenie w teorii całkowania ułamków wymiernych.

Każdy ułamek właściwy

P(x)

G(*)

można przedstawić w postaci sumy skończonej liczby ułamków prostych.