0054

56

VIII. Funkcja pierwotna (całka nieoznaczona)

Dla obliczenia całki

dx

/ (ax² + óx+c)<²"+‘>'² “ / y(2m+l)/2 najdogodniej będzie użyć tak zwanego podstawienia Abela

Y'    ax + \b

2]/y j/ax²+óx+c Podnosząc do kwadratu i mnożąc przez 4Y otrzymujemy równość 4t²7 = (7')² = 4a²x²+4aóx+ó² , którą odejmiemy od pomnożonej przez 4a równości

y = ax² + bx+c.

W wyniku otrzymujemy

4 (a — t²) Y = 4ac—b² ,

skąd

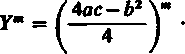
1

(a-t²y '

(10)

Różniczkując teraz równość

t |/y = ax + t ó

znajdujemy

|/y dt + t²dx = a dx,

a więc (11)

dx dt

W~ ^a~^t2'

Z (11) i (10) otrzymujemy i wreszcie

(¹²>    / yita+uża = (ąac-ó²') / <^a “ *    ^dU

Tak więc całe zadanie sprowadza się do obliczenia całki z wielomianu.