0052

54

VIII. Funkcja pierwotna (całka nieoznaczona)

m ^ 1, obliczmy pochodną

(x^m~ⁱ\/Y)' = (m-l)x^m-²^Y + -- jl-

2/y

2 (m — 1) x^m~²(ax² + bx + c)+x^m~¹(2 ax + b)

2 ]/Y

= ma ^:T— + | m—y ) b^x _ +(m-l) c ■ ²)    1/Y

x*

Vy

\/Y    ' V*

i scałkujmy otrzymaną tożsamość; otrzymamy

x^m~¹\/Y = maV_m+ (m-±) bYn-i+im-l) cV_m-₂ . Biorąc tu m = 1 znajdziemy

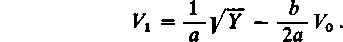
Biorąc następnie m = 2 i wykorzystując wyrażenie dla V_l otrzymujemy V₂ = -^(2^-36) ]/y + JL(3b²-4ac) V₀ .

Postępując tak dalej dojdziemy do ogólnego wzoru

V_m = p_m-i(x) ]/Y +A_m V₀ ,

gdzie p_m__x (x) jest wielomianem stopnia m — 1, a A_m = const. Tak więc wszystkie całki V_m sprowadzają się do V₀.

Jeżeli w całce I wielomian P (x) będzie stopnia n, io całka ta będzie kombinacją liniową całek V₀, V₁,..., V_n, a więc na mocy poprzedniego wzoru można ją napisać w postaci

⁽⁹⁾    fw-^JX=eM,/7+ifw’

gdzie Q (x) jest pewnym wielomianem stopnia n— 1, a A = const.

Samo wyznaczenie wielomianu Q (x) i stałej A dokonuje się zwykle metodą współczynników nieoznaczonych. Różniczkując (9) i mnożąc obie strony otrzymanej równości przez )/Y otrzymujemy

P(x) = Q'(x)(ax² + bx + c)+ y Q (x) (2ax + b) + A.

Jeśli zamiast Q (z) podstawimy tu wielomian stopnia n— 1 o współczynnikach nieoznaczonych, to otrzymamy po obu stronach wielomiany stopnia n. Przyrównując współczynniki