P1111251

8 VIII. Funkcja pierwotna (całka nieoznaczona)

264. Całka i obliczanie pola. Znacznie ważniejsza jest interpretacja funkcji pierwotnej jako pola figury krzywoliniowej. Ponieważ pojęcie funkcji pierwotnej było historycznie blisko związane z zadaniem obliczania pola, zajmiemy się tym zadaniem już teraz, korzystając z intuicyjnego pojęcia pola figury płaskiej i odkładając ścisłe sformułowanie zagadnienia do rozdziału X.

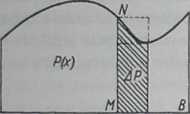
Niech w przedziale (a, b) będzie dana funkcja ciągła y = f(x) przyjmująca tylko dodatnie (nieujemne) wartości. Rozpatrzmy figurę'AB CD (rys. 2), ograniczoną przez krzywą y = /(x), dwa odcinki prostych x = a \ x = b oraz odcinek osi x; figurę tego typu nazywamy trapezem krzywoliniowym. Chcąc określić wielkość pola |P) tej figury, zbadajmy

zachowanie się pola zmiennej figury AMND zawartej między prostą początkową x = a i prostą pionową odpowiadającą dowolnej wartości x z przedziału <a, b>. Przy zmianie x to ostatnie pole będzie się również zmieniało, przy czym każdemu x odpowiada w pełni określona wartość pola, a więc pole trapezu krzywoliniowego AMND jest pewną funkcją zmiennej x. Oznaczmy tę funkcję za pomocą symbolu \P (x)|.

A

D

C

Rys. 2

x x+Ax b x

0 a

Postawmy sobie najpierw za zadanie znalezienie pochodnej tej funkcji. W tym celu nadajmy zmiennej x pewien przyrost Ax, na przykład dodatni. Wówczas pole |P(x)| otrzyma przyrost \AP\.

Oznaczmy przez m i M odpowiednio najmniejszą i największą wartość funkcji /(x) w przedziale <x, x+dx> [85] i porównajmy pole \AP\ z polami prostokątów zbudowanych na podstawie Ax i mających wysokości m i M. Oczywiście

mAx < \AP\ < MA x,

skąd

Jeśli Ax -¹■ 0, to dzięki ciągłości funkcji /, zarówno m jak i M będą dążyły do/(x) i dlatego

|f(x)l = limJ^- = /(x).

4¹-0 PU

Tak więc doszliśmy do znanego twierdzenia nazywanego zwykle twierdzeniem Newtona i Leibniza (¹):

Pochodna pola zmiennego |P(x)| względem odciętej końcowej x jest równa rzędnej końcowej y - /(x).

Innymi słowy, pole zmienne | P (x)| jest funkcją pierwotną danej funkcji y = f(x). Spośród wszystkich innych ta funkcja pierwotna wyróżnia się tym, że jest równa zeru dla x — a. Jeśli więc znamy jakąkolwiek funkcję pierwotną F (x) funkcji /(x), to na mocy twierdzenia z poprzedniego ustępu

|F(x)| | F(x)+C,

gdzie stałą C można łatwo wyznaczyć podstawiając x = a:

0 = F(a)+C,

skąd

C = -F(a).

Ostatecznie więc

|F(x)| - F(x)—F(a).

W szczególności, aby otrzymać pole P całego trapezu krzywoliniowego ABCD, trzeba wziąć x *= b, a więc

|F| =' F(b)—F(a).

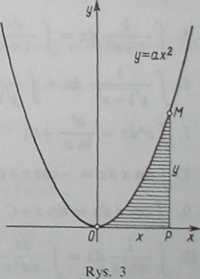
Obliczmy na przykład pole P(x) figury ograniczonej parabolą y = ax*, rzędną odpowiadającą danej odciętej x i odcinkiem osi x (rys. 3). Ponieważ parabola przecina oś x w początku współrzędnych, wartość początkowa x jest 0. Dla funkcji f(x) = ax² łatwo znaleźć funkcję pierwotną F(x) = \ax*. Funkcja ta jest równa zeru właśnie dla x = 0, a więc

|P(x)| = F (x) = ax³ = y xy [porównaj 32,4)].

Wobec związku zachodzącego między obliczaniem całek i obliczaniem pól figur płaskich, tj. ich kwadraturą, przyjęte jest nazywać kwadraturą również samo obliczanie całek.

Aby rozszerzyć wszystko co powiedziano wyżej na wypadek funkcji przybierającej także wartości ujemne, wystarczy przyjąć umowę, że będziemy uważali za ujemne części figury położone pod osią x.

Tak więc jakąkolwiek funkcję/(*) ciągłą w przedziale <a, 6) będziemy rozpatrywali, czytelnik może sobie zawsze wyobrażać jej funkcję pierwotną jako zmienne pole figury ograniczonej wykresem danej funkcji. Nie można jednak, rzecz jasna, uważać tej ilustracji geometrycznej za dowód istnienia funkcji pierwotnej, ponieważ samo pojęcie pola nie zostało jeszcze ściśle zdefiniowane.

W następnym rozdziale [305] będziemy w stanie dać ścisły i przy tym czysto analityczny dowód tego ważnego faktu, że każda funkcja f(x) ciągła w danym przedziale ma w nim funkcję pierwotną. Twierdzenie to przyjmujemy już teraz, na razie bez dowodu.

W tym rozdziale będziemy mówili o funkcjach pierwotnych tylko funkcji ciągłych.

1

W rzeczywistości twierdzenie lo, co prawda w innej formie, opublikował jeszcze Izaak Barrow, na uczy ód Newtona.