0006

VIII. Funkcja pierwotna (całka nieoznaczona)

264. Całka i obliczanie pola. Znacznie ważniejsza jest interpretacja funkcji pierwotnej jako pola figury krzywoliniowej. Ponieważ pojęcie funkcji pierwotnej było historycznie blisko związane z zadaniem obliczania pola, zajmiemy się tym zadaniem już teraz, korzystając z intuicyjnego pojęcia pola figury płaskiej i odkładając ścisłe sformułowanie zagadnienia do rozdziału X.

Niech w przedziale <a, by będzie dana funkcja ciągła y = f(x) przyjmująca tylko dodatnie (nieujemne) wartości. Rozpatrzmy figurę' ABCD (rys. 2), ograniczoną przez krzywą y = f(x), dwa odcinki prostych x — a i x = b oraz odcinek osi x; figurę tego typu nazywamy trapezem krzywoliniowym. Chcąc określić wielkość pola |P| tej figury, zbadajmy

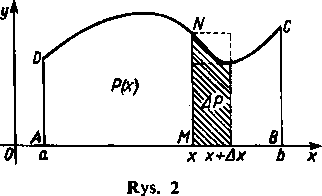
zachowanie się pola zmiennej figury AMND zawartej między prostą początkową x = a i prostą pionową odpowiadającą dowolnej wartości x z przedziału <a, by. Przy zmianie x to ostatnie pole będzie się również zmieniało, przy czym każdemu x odpowiada w pełni określona wartość pola, a więc pole trapezu krzywoliniowego AMND jest pewną funkcją zmiennej x. Oznaczmy tę funkcję za pomocą symbolu |P(x)|.

Postawmy sobie najpierw za zadanie znalezienie pochodnej tej funkcji. W tym celu nadajmy zmiennej x pewien przyrost Ax, na przykład dodatni. Wówczas pole |P(x)| otrzyma przyrost \AP\.

Oznaczmy przez m i M odpowiednio najmniejszą i największą wartość funkcji f(x) w przedziale <x, x+Axy [85] i porównajmy pole \AP\ z polami prostokątów zbudowanych na podstawie Ax i mających wysokości mi M. Oczywiście

mAx < \AP\ < MA x,

skąd

m < <M.

Jeśli Ax

0, to dzięki ciągłości funkcji /, zarówno m jak i M będą dążyły do /(x) i dlatego \P'(x)\ = lim-^- = /(x).

4x-0 AX

Tak więc doszliśmy do znanego twierdzenia nazywanego zwykle twierdzeniem Newtona i Leibniza (¹):

Pochodna pola zmiennego |P (jc)| względem odciętej końcowej x jest równa rzędnej końcowej y = /(¹).

W rzeczywistości twierdzenie to, co prawda w innej formie, opublikował jeszcze Izaak Barrow, nauczycie] Newtona.