Image0095 BMP

9.8.2. Ogólny wzór dli utrat wlroprądowych

Rozpatrzmy przedstawiony na rys. 8.2 odcinek elementarny przewodu, w którym [dynie prąd /=/*. Normalny względem powierzchni przewodu wektor ds skierowany do jego wnętrza, czyli przeciwnie niż wektor dS na rys. 8.2 określony jest wzorem

ds= — dXxdI,

przy czym dk = l,dx oraz dl = ],d/, gdzie wektor jednostkowy J₍ jest styczny do brzegu przekroju poprzecznego przewodu, a dl jest równoległy do osi przewodu {rys. 8.2).

Wzór (9.120) dla strumienia mocy zespolonej wypływającej z wnętrza przewodu przy* biera zatem postać

$k~ f QE_f ■ H*] ■ [di. x dl], k = l, 2.....n.    (9.123)

Iloczyn skalarny dwóch iloczynów wektorowych zawarty w zależności (9.123) wyraża się wzorem (por. p.8.5.2)

(E, • dk)(H* • dl) - (E_f • dl)(H* • dk)= - (E, • dl)(H* ■ d>.),

bowiem w rozpatrywanym przypadku wektor Ej jest równoległy do osi przewodu, a więc jest prostopadły do dk. Wyrażenie (9,123) można zatem przedstawić w postaci

J[;fH*-dk]E_i*dl,    (9.124)

c»

przy czym drogami całkowania całek są: krzywa brzegowa przekroju poprzecznego przewodu oraz linia C_k znajdująca się na jego powierzchni.

Na podstawie prawa przepływu otrzymujemy

$H*-d 1=/?,

bowiem wnętrze krzywej brzegowej przekroju poprzecznego przewodu przenika prąd [_k. Wobec tego wyrażenie (9.124) przybiera postać

S_t=~lJ fEj-dl, k—l, 2, ...,    n.    (9.125)

c_k “

Całka zawarta w zależności (9.125) przedstawia siłę elektromotoryczną indukowaną wzdłuż przewodu k przez prądy płynące we wszystkich przewodach. Wielkość tę można obliczyć przy zastosowaniu zasady superpozycji, otrzymując

jEj-dl =-Z*I*- t Z,_H/„    (9.126)

c*    i= i

i*k

zgodnie z podanym w p. 8.5 określeniem impedancji wzajemnej i zewnętrznej przewodów, przy czym Z_tk oznacza impedancję zewnętrzną przewodu k, zaś Z_ki — impedancję wzajemną przewodów k, i, Należy zwrócić uwagę, że wielkości te przybierają wartości zespolone o różnej od zera części rzeczywistej, co jest wynikiem oddziaływania prądów wirowych w ścianie metalowej. Omawiane impedancję wyrażają się liczbami urojonymi przy pominięciu oddziaływania prądów wirowych, a więc gdy przewody znajdują się w dużej odległości od ściany metalowej.

Podstawiając zależność (9.126) do w/oru (9.125), mamy

S* = ?_ek/₍^J4- £ Z*,Vr, fc= 1,2(9.127)

i ^Ł 1 i*JŁ

bowiem ĄI*=,/ł, wobec czego

Ż & = i 2_ekli+ i i    (9.128)

*=1    t = l    S-l 1-1

IWfc

Powyższe wyrażenie można przedstawić w postaci macierzowej

n

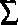
	z.i z]3 ... zIfl
	?21 Z'2 ... Zia		/a
	_?.i Z„2 ... Z„		Li.

(9.129)

przy czym Z_a=Z_ti, wobec czego macierz kwadratowa zawarta w otrzymanej zależności jest symetryczna.

Zgodnie ze wzorem (9.122), straty wiroprądowe P są równe części rzeczywistej

M

mocy zespolonej £ S_k. Wyodrębniając część rzeczywistą wyrażenia (9.128) lub (9.129), otrzymujemy w wyniku

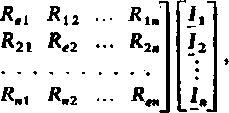
(9.130)

MI?.?*,-

przy uwzględnieniu, że

Zuhl*+Z_tt I_k 1*=Z_ki 2Re(/|/*)=(Z_łl+Z_tt) R e(/,I?),

bowiem 1J%+/*/*=2Re (/,/*). Wielkości R_rk oraz R_ki przedstawiają odpowiednio rezystancję własną przewodu k oraz rezystancję wzajemną przewodów k, i, określone za pomocą wzorów

(9.131)

•Rft—Re (Z_rt),

P-ki *= ^^C(Zjfci),

przy czym R_lk^R_kl.

W przypadkach szczególnych otrzymuje się wzory następujące: — dla symetrycznego układu trójfazowego:

P = (Pe 1 +-Re2 + ^ł3“^12 ^—^23“"^3l)^² >

—    dla układu jednofazowego:

P=(R_fI+R,₂-2R₁₂)/²,

—    dla pojedynczego przewodu:    ł