skanuj0002 (105)

84 RACHUNEK PRAWDOPODOBIEŃSTWA

TWIERDZENIE O PRAWDOPODOBIEŃSTWIE CAŁKOWITYM # Jeżeli zdarzenia H\, H₂,..., H_nczQ są takimi zdarzeniami, że

1)    HiC\Hj=0 dla i=Aj (są parami rozłączne)

2)    P(Hk)>0 dla każdego ke {1,2,n}

3)

to dla dowolnego zdarzenia A <z £2: P(Ą)=P(A /Hj) ■ P(H\)+P(A /H₂) ■ P(H₂) +... + P(A IH_n) ■ P(,H„).

ZADANIA WPROWADZAJĄCE

6.1

Oblicz a) 4!; b) —;

c)

d) —: 8!

e)

3!-5!

(701.    g) ^31!~^3Q!

'    9! ’    291 + 28!

6.2

Sprowadź do prostszej postaci wyrażenie

a)

n!+(« +1)!.

(n-1)! *

c) (2n)! + (2n-l)! + (2n-2>l

6.3

6.4

(/»+2)!. n\

b)

Oblicz a)

	^ f^20l	v (lA	(13)
Uf	^b> m	^c)U^;	^d) u>	^e,U

b)

Tn + 6'l

l ² J

Rozwiąż równanie lub nierówność

10;

28;

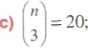
d)

	(^5) 1
(n} „	UJ j
<21; UJ	^e) 7T^>^ HJ
	UJ i

Zdający potrafi	• obliczać wartości n! i 1 W

Zdający potrafi

obliczać współczynniki rozwinięcia dwumianu Newtona korzystać z dwumianu Newtona w rozwiązywaniu zadań

6.5    Wyznacz rozwinięcie dwumianu Newtona (x+1)⁵.

6.6    Oblicz współczynnik przy x⁷ w rozwinięciu dwumianu (x+ 1 )⁹.

6.7    Znajdź środkowy wyraz rozwinięcia dwumianu (yfl +x)⁸.

6.8    Ile wyrazów wymiernych występuje w rozwinięciu dwumianu (V2 + ^3)'°°?

Zdający potrafi

•    stosować wzory na liczbę: permutacji, kombinacji oraz wariacji z powtórzeniami i bez powtórzeń

•    rozwiązywać zadania tekstowe z zastosowaniem wzorów kombinatorycznych

6.9 W pewnym liceum są dwie klasy trzecie: IIIA i IIIB. W IIIA jest 10 dziewcząt i 20 chłopców, a w klasie IIIB 18 dziewcząt i 8 chłopców. Spośród maturzystów należy wybrać dwie osoby - po jednej z obu klas, które zaproszą dyrekcję szkoły na studniówkę.

a)    Na ile sposobów można dokonać wyboru takiej pary uczniów?

b)    Na ile sposobów można dokonać takiego wyboru, aby wśród wybranych osób były dwie dziewczyny?

c)    Na ile sposobów można dokonać takiego wyboru, aby wśród wybranych osób byli maturzystka i maturzysta?

6.10    Dany jest zbiór A = {1, 2, 3, 4, 5}. Oblicz liczbę wszystkich

a)    czterowyrazowych ciągów o wyrazach należących do zbioru A;

b)    trój wyrazowych ciągów o różnych wyrazach ze zbioru A;

c)    dwuelementowych podzbiorów zbioru A.