img144 (2)

4. Przekształcenie Fouriera i jego właściwości.doc, 1/10

ANALIZA WIDMOWA SYGNAŁÓW NIEOKRESOWYCH

sygnał okresowy x(r), o okresie T można rozwinąć w przedziale nieskończonym (-00,00) szereg trygonometryczny lub wykładniczy

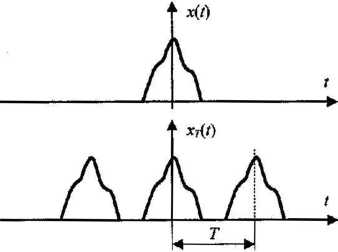
w praktyce analizie częstotliwościowej poddawane są sygnały ograniczone w czasie oraz na ogół nieokresowe potrzeba stworzenia narzędzi analitycznych do badania dowolnych sygnałów, w tym nieokresowych^ o dowolnym czasie trwania rozpatrzmy dowolny ograniczony w czasie sygnał nieokresowy x(t) oraz jego okresowe powielenie x_r(/)

4. Przekształcenie Fouriera i jego właściwości.doc, 2/10

ANALIZA WIDMOWA SYGNAŁÓW NIEOKRESOWYCH (cd)

przy założeniu, że okres T dąży do nieskończoności

lim x_T

sygnał x_T(t) można zapisać w postaci

x_Ti‘)= X*(/+«r)

żi=-QO

ponieważ x_T(t) jest sygnałem okresowym można go rozwinąć w przedziale nieograniczonym w wykładniczy szereg Fouriera

*j (')= Z ,gdzie co₀ = ~

l~-a>    *

współczynniki rozwinięcia