s0005 (5)

jeoria Sygnałów - KOLOKWIUM
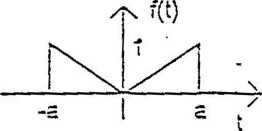
.') Zademonstrować użycie wybranego (jednego lub wiece;) twierdzenia / dla transformaty Fouriera do wyznaczenia widma pokazanego na rysunku sygnału u(t). Twierdzenia nie trzeba udowadniać. (1,5 pc)
. Znaleźć wszystkie wartości parametru a, dla których pokazany na rysunku sygnał okresowy zlatany z impulsów Diraca nie posiada 15. harmonicznej (1,5 pc)
\.
(bO
!r-
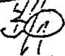
/N
I | v~ I ■/
-T12 1_L? T/2 t
>
^ Wyznaczyć transformatę -Fouriera sygnału u(r) = 5 cos (2:) -2 sin (3c) •
, ■ Narysować odpowiednie- widmo amplitudowe. W przypadku użycia jakichkolwiek rwierdzen dla transformaty Foimera/należy je udowodnić. (2 pt)
Si} ćr(o~^J g[gKJ
Cs
O
— 1 -a
7
Wyszukiwarka
Podobne podstrony:
s0034 eóric Sygnałów - KOLOKWIUM 1. Podać pełna postać twierdzenia ?anevaia d c sygnałów pjeokresowy
s0030 i eoria Sygnałów - KOLOKWIUM 1. Podać pełną postać twierdzenia ParsevaJa dla sygnałów nieokres
s0079 Teoria Sygnałów - KOLOKWIUM 1. Podać pełną postać twierdzenia ParsevaJa dl
s0006 (5) ~ Teoria Sygnałów i KOLOKWIUM i. Podać pełną postać twierdzenia dla szeregu Fouriera o ilo
s0029 Teoria Sygnałów - KOLOftmWl" 1. Podać pełną postać twierdzenia ParsevaJ
s0078 eoria Sygnałów - KOLOKW1UM 1. Podać pełną postać r^erdzenia Panevz!z di?, sygnałów ni eokres o
tsk1006 Teoria Sygnałów KOLOKAYIUM 1. Podać pełną postać twierdzenia aia szeregu F
tsk1013 Teoria SygnałówKOLOKWIUM 1. Podać pełną postać twierdzenia Parsenaia dia zespolonego sz (1
tsk1010 feeria Sygnałów - KOLOKWIUM Podać re-lnn n-ostac t.v:crczen:a Parsevaia c;a svzna?ow nieezre
s0049 OpO o J •» • J —Teoria Sygnałów - KOLOKWIUM L Podać, wraz z wyprowadzeniem., wzór opisujący
więcej podobnych podstron