Image32

62

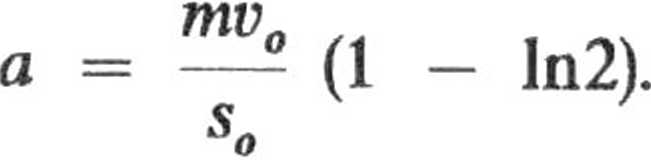
Na siłę hamującą F , działającą w chwili początkowej, otrzymujemy więc

wyrażenie

F. =

^2mv0 ₍₁

- In2)

2.2. Równanie ruchu samochodu przybiera postać

m

dv

dt

— kv²

Całkując to równanie metodą rozdzielenia zmiennych, przy warunkach początowych: y(0) = v_a, x(0) = 0, otrzymujemy

mv

v =

k t + m ’

m , k v_n t + m

- In -

k    m

t, =

Stąd znajdziemy czas t_t, po którym prędkość sai ^m , i odpowiadającą mu drogę

ochodu zmaleje do połowy,

m

x(t_i) = — ln2.

k

2.3. Niech oś x będzie skierowana do góry. Wtedy siła ciężkości ma zwrot przeciwny niż oś, tak że F_l — —mg; wektor prędkości ma taki sam zwrot jak siła ciężkości, a siła hamująca jest skierowana zgodnie z osią, tj. F₂ = mkv, gdzie k jest stałą dodatnią. Zatem równanie ruchu przybiera postać

dv

dt

= ~(g - M-

Całkując je dwukrotnie metodą rozdzielenia zmiennych, przy warunkach początkowych: r(0) = 0, x(0) = h, otrzymujemy

Gdy opór ośrodka jest bardzo mały, wówczas funkcję / = 1 — e** można rozwinąć w szereg Maclaurina.

1

1

1

m « /(O) 4- - /'(O) t 4- - /"(O) t² + - /'"(O) f³ + ... -

1!

2!

3!

kt

- j k³1³ +

O

Biorąc cztery początkowe wyrazy rozwinięcia i wstawiając do wzoru na drogę, dostajemy przybliżone wyrażenie na x(t)

2.4. Cząstka naładowana porusza się w zadany ruchu

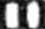
polu zgodnie z równaniem

q E₀ sin cot.

a. Przy podanych warunkach początkowych otrzymujemy

MO =

9 E,

mco

(i

coscot),

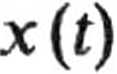
q ^Eo •

-y sincot 4-

ma)

<ł ^Eo

ma)

Rozwiązania powyższe przedstawiono na rys. 17.

b. Podstawiamy rozwiązanie próbne x(t) = x_l sincut 4- v_Qt 4- do równania ruchu. Równanie to będzie spełnione, gdy

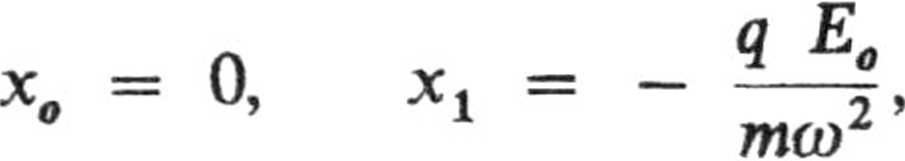
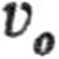
g ^Eo

mco