img067 (6)

9

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera (cd)

•    podane powyżej definicje można uogólnić na układ ortogonalnych funkcji zespolonych

•    warunek ortogonalności dla układu funkcji zespolonych zapisuje się następująco

h

= 0 dla i * j_t gdzie i,j = 0,1,2,...

'i

kwadrat normy jest równy

KII² = rW“’W*= ]HĄ²dt

współczynniki uogólnionego szeregu Fouriera dla układu ortogonalnych funkcji zespolonych wyznacza się z następującego wzoru

10

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera (cd)

•    uogólniony szereg Fouriera posiada bardzo istotną, przedstawioną dalej, właściwość

•    dla sygnału x(r) wprowadzimy skończenie wymiarową aproksymację w postaci

n

*W=2>K)

/=0

gdzie:

i/,(r)    - wybrany układ funkcji ortogonalnych (funkcje bazowe)

c_j - współczynniki rozwinięcia

• powyższy szereg zapewnia najlepszą aproksymację w sensie minimum błędu średniokwadratowego, jeżeli współczynniki c_t zostaną wyznaczone według

wzoru

|2

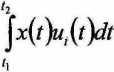
^ai =