img192

7. Sygnał wąskopasmowy.doc, 1/20
SYGNAŁY WĄSKOPASMOWE
Sygnały o ograniczonym paśmie
• odtworzenie czasowej postaci sygnału wymaga uwzględnienia wszystkich składowych jego widma w przedziale nieograniczonym; z fizycznego punktu widzenia jest to operacja nierealizowalna
• przy założeniu, że energia sygnału jest skończona, wkład składowych widma, przy co co , jest pomijał nie mały; ponadto każde urządzenie fizyczne przeznaczone do przesyłania i przetwarzania sygnałów ma skończone pasmo przepustowe
• sygnały, których widma są różne od zera jedynie w pewnym przedziale o skończonej długości, nazywamy sygnałami o ograniczonym paśmie
• jeżeli T jest skończonym przedziałem pulsacji, wówczas widmo sygnału o ograniczonym paśmie można zapisać w postaci
J(T(g))^0 dla co€ T X(co)=0 dla to£ r
• ogólny model matematyczny sygnału o ograniczonym paśmie
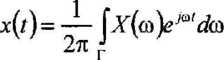
7. Sygnał wąskopasmowy.doc, 2/20
SYGNAŁY WĄSKOPASMOWE (cd)
Przykład 1 idealny sygnał dolnopasmowy (o widmie rzeczywistym)
X0 dla |co|<co„,
dla M = <0»
[ 0 dla |<o|><■>».
czasowa postać sygnału
Ax(t)
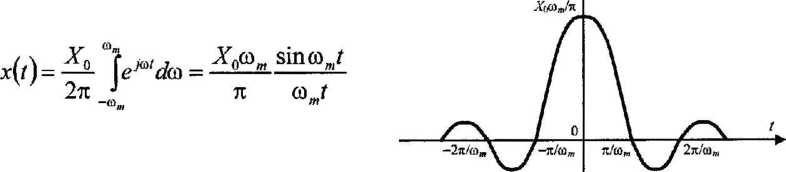
Wyszukiwarka
Podobne podstrony:
img193 (4) 7. Sygnał wąs kopasmowy.doc, 3/20SYGNAŁY WĄSKOPASMOWE (cd) idealny sygnał dolnopasmowy (o
img196 (5) 7. Sygnał wąskopasmowy.doc, 9/20SYGNAŁY WĄSKOPASMOWE (cd) obwiednię zespoloną możemy prze
img199 (4) 7. Sygnał wąskopasmowy.doc, 15/20SYGNAŁ ANALITYCZNY (cd) zatem równość określająca widmo
img194 (4) 7. Sygnał wąskopasmowy.doc, 5/20SYGNAŁY WĄSKOPASMOWE (cd)Sygnały wąskopasmowe •
img195 (4) 7. Sygnał wąskopasmowy.doc, 7/20SYGNAŁY WĄSKOPASMOWE (cd) - zespolony model (III) sygnału
img197 (4) 7. Sygnał wąskopasmowy.doc, 11/20SYGNAŁ ANALITYCZNY fundamentalnym zagadnieniem w analizi
img198 (4) 7. Sygnał wąskopasmowy.doc, 13/20SYGNAŁ ANALITYCZNY (cd) zatem sygnał analityczny można p
65386 img201 (2) 7. Sygnał wąskopasmowy.doc, 19/20SYGNAŁ ANALITYCZNY (cd)Właściwości przekształcenia
85960 img200 (2) 7. Sygnał wąskopasmowy.doc, 17/20SYGNAŁ ANALITYCZNY (cd) można również wyrazić sygn
więcej podobnych podstron