MATEMATYKA049

90 U Ciąg/ i izeirgi liczbowe

2 Suma S- lim S„; a)l, h)2, c) nie istnieje, d)+oo, e) me istnieje. f)l

n ^

3, Wystarczy pokimać, żc lim «„ *0 lub lim n_n mc istnieje o)B_n -»2. b)a_ n-*w>    o--**'¹

c) cios (a_n) rozbieżny, gdyż. «j.-*l.*j» r*-l.    d)«_n-»1, c) «„-►!,

0 ciąg (*„) rozbieżny.

4    j«(-l;l),Sr-~.    h)~;n-yq^-|, c) 48; n*24,q-i,

d)-i ® ,a«3>0,qa2>l. c)2,n ^ j.q , f)suma mc iHlmejc,q = -2<-1

5.    a) /.bieżny, b) rozbieżny, c) zbiezny. d) zbieżny, c) zbieżny, f) zbieżny.

6.    a) Zbieżny, b) zbieżny, c) rozbieżny, d) zbieżny, c) rozbie/ny, 0 zbieżny

7.    a) Zbieżny; b) zbieżny, c) rozbieżny, d) zbieżny, c) rozbieżny, 1) rozbieżny,

g) zbieżny, h) rozbieżny, i) zbieżny, j) rozbieżny, k) rozbieżny, 1) zbieżny

9. a) Bezwzględnie zbieżny, d) bezwzględnie zbieżny, g) warukowo zbieżny,

j) bezwzględnie zbieżny,

1) warunkowo zbieżny, o) rozbieżny.

b)    bezwzględnie zbieżny,

c)    rozbieżny,

h) bezwzględnie zbiezny,

k) bezwzględnie zbieżny,

m) warunkowo zbieżny, p) rozbieżny,

c) bezwzględnie zbieżny, 0 warunkowo zbieżny,

i) bezwzględnie zbieżny,

1) rozbieżny,

n) bezwzględnie zbiezny,

r) bezwzględnie zbieżny.

10 a) Rozbieżny, c) rozbieżny, i) rozbieżny. 1) zbieżny, p) zbieżny.

u) rozbieżny

b) rozbieżny, 0 zbieżny,

j) rozbieżny,

m) zbieżny, r) zbieżny,

c) rozbieżny, g) zbieżny,

k) rozbieżny,

n) rozbieżny,

s) zbieżny.

d) rozbieżny, h) zbieżny,

I) rozbieżny,

o) rozbieżny,

t) rozbieżny.

II a) Rozbieżny. ( £n„ zbieżny ) ^>(a_n->0) >(—-»+« *())=> (£-L rozbieżny ).

a„    a.

b) zbieżny, c) zbieżny n-J 1

n.r- 3ⁿ

I2.(    >^:    Z ~_n* iloczyn Cauchy'cgo dwu s/crcgbw' oraz j^{C!łl to}

. • II II    I 1 n-1    £ I I

vcrcgIc_B,gd/.cc_n^—4~^_T+-..żż^._I-^_n-dlanS2ora/l^ = ₃-

2"

14 u) 0, szereg jest zbieżny (kr d'Alcmber1a), więc a_n -♦0,

b) ■*■<». szereg £~ⁿ'- jest zbieżny, więc — -*0. więc ~żr~* n"    n"    ⁿ

n

n

b)    <-2/3, 2/3),    c)( ®,-l>u<l,+»).

c)    0; szereg

15. a)Kl),

d)    <0.1).

c) (2/3,4/3>,    0(-ae,-2>u(0, ♦<»)

3. CIĄGI I SZEREGI LICZBOWE O WYRAZACH ZESPOLONYCH

Ciągi o wyra/acii zespolonych Dla ciągu (a_n). którego wyrazy są liczbami zespolonymi definicja granicy jest dokładnie taka. jak dla ciągu o wyrazach rzeczywistych:

Z AVA i*

09 K n>K ⁰

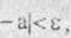
(lima_n = a)

n-+*>

Oznacza to, żc ciąg (a_n) o wyrazach zespolonych ma granicę a, gdy w dowolnie wy branym otoczeniu punktu a (tzn. wewnątrz okręgu o środku w punkcie a i dowolnym promieniu e) leżą prawic wszystkie wyrazy tego ciągu

Granice ciągów o wy razach zespolonych obliczamy podobnie, jak ciągów o wyrazach rzeczywistych. Jeśli wyrazy ciągu zapisane są w postaci kartezjańskiej, możemy stosować następujące twierdzenie:

TWIERDZENIE 3.1 Ciąg o wyrazie ogólnym a_n = et,, + ip_n jest zbieżny wtedy i tylko wtedy, gdy ciągi (a.) oraz (P_#) są zbieżne, przyczyni

(hm(a_n+ ipj = a + iP)o(hma_n -a a limP_n - P)-

n ►*»    n »•©

Jeśli więc ciąg (a„) lub (P_n) jest rozbieżny, to ciąg (a_n) jest również rozbieżny.