P1160450

Z kolei, jeśli opór tkaniny filtracyjnej można pominąć, to równanie (3.47) upraszcza się do postaci:

(3.49)

Przy spełnieniu obydwu założeń (osad nieściśliwy i opór przegrody filtracyjnej po-mijalnie mały) otrzymuje się równanie:

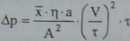
(3-30)

3.2.4. Filtracja dwuetapowa

Jeśli proces filtracji plackowej wykonuje się dwuetapowo, tzn. początkowo przy sta-łej szybkości filtracji, a od pewnego momentu przy stałym ciśnieniu, to równanie opisujące drogi etap filtracji dwuetapowej przybiera postać:

V^j-V,^j+2C(V-V,)-K(t-t,)    (3.51)

gdzie:

V, - objętość filtratu otrzymana w pierwszym etapie procesu. m\

T| - czas trwania pierwszego etapu filtracji, s.

Czas trwania pierwszego okresu filtracji dwuetapowej i objętość filtratu otrzymane w pierwszym etapie filtracji związane są równaniem:

(3.52)

V*| V, __ K tj, " t, * 2*(C +V,)

Objętość filtratu otrzymaną w pierwszym etapie filtracji oblicza się ze wzoru:

V,

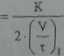
-c

(3.53)

Czas trwania pierwszego etapu filtracji dwuetapowej oblicza się z zależności:

w

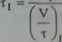
0-54)

Zależność określająca szybkość procesu filtracji w wirówce filtracyjnej ma postać:

dV it-tp² -p_t -H zj-zj

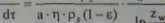
ln—

(335)

gdzie:

dV/dx - szybkość filtracji, m³/s,

0) - prędkość kątowa, rad/s, p_c — gęstość zawiesiny, kg/m³,

H - wysokość bębna wirówki, m, a — opór właściwy osadu, kg/m,

T) - lepkość filtratu, Pa- s,

Ps — gęstość ciała stałego, kg/m³,

Zw - promień bębna wirówki, m,

Zo - promień wewnętrzny walca cieczy w wirówce, m, zi - promień zewnętrzny walca cieczy w wirówce, m

4. Transport ciepła

4.1. Przewodzenie ciepła

Ustalone przewodzenie ciepła, tj. przewodzenie ciepła, gdy pole temperatur nie zależy od czasu, opisane jest przez równanie Fouriera, które dla przewodzenia jednokienm-kowego i dla wybranego kierunku osi x-ów ma postać:

(4.1)

Q.-X.a£

gdzie:

Q - strumień ciepło przewodzonego w kierunku osi x. W,

X - współczynnik przewodzenia ciepła, W/(m- K),

A - powierzchnio przekroju prostopadła do kierunku ruchu ciepła, m. dt/dx - gradient temperatury w kierunku osi x, K/m.