PB032275

%

granica ciągu liczbowego

139

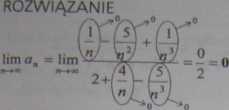
$ PRZYKŁAD 2.79

3 n² — Sn+ 4 n + 6

Oblicz granicę ciągu o wyrazie ogólnym a_n = —

ROZWIĄZANIE

lim a„ = lim

CO

- =00

Gdy n -> co, licznik rośnie nieograniczenie, a mianownik dąży do 1, więc dany ciąg ma granicę co.

■

Zastosowanie w przykładach 2.75—2.79 metody obliczania granicy dowolnej funkcji wymiernej zmiennej n pozwala sformułować następujący wniosek:

WNIOSEK:

1.    Jeżeli licznik i mianownik ułamka są wielomianami tego samego stopnia względem zmiennej naturalnej n, to granica takiego ułamka przy n -» co równa się ilorazowi współczynników przy najwyższych potęgach n.

2.    Jeżeli mianownik ułamka jest wielomianem stopnia wyższego niż licznik, to granica tego ułamka przy n -» oo jest równa zeru.

3.    Jeżeli licznik ułamka jest wielomianem stopnia wyższego niż mianownik, to gdy n oo, wartość bezwzględna ułamka dąży do nieskończoności.

i O PRZYKŁAD 2.80

Oblicz granicę ciągu o wyrazie ogólnym a_n =/i—>/n² +5/i.

ROZWIĄZANIE

Odjemna, jak i odjemnik, rosną nieograniczenie ze wzrostem n, zatem mamy do czynienia z wyrażeniem nieoznaczonym typu: „oo - oo”. Przekształcamy to wyrażenie, korzystając z następującego wzoru:

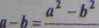
a + b