PC043386

84

Przykład 1*75

Rozwiązując równanie Zr-3=6(r - 2) + 5, dokonujemy równoważnych pr*. kształceń tego równania:

2x - 3 = 6(r — 2) + 5,

2jc - 3 = 6x - 12 + 5_t 2r - 6x = -7 + 3,

- 4r = -4 : (^1),

otrzymując ostatecznie jedno rozwiązanie x = 1.

Definicja 1.66. Nierównością liniową z jedną niewiadomą nazywały każdą z nierówności postaci: ax + b >0, ax + b <0, coc + b> 0, ax + bś\$ gdzie ay&e R.

W zależności od stałych a i b zbiorem rozwiązań nierówności liniowej może być: przedział nieograniczony (dla a 0). zbiór liczb rzeczywistych lub zbiór pusty.

Rozwiązywanie nierówności liniowej prowadzimy podobnie jak w przypadła ■ równań, pamiętając jednak o tym, że przy mnożeniu i dzieleniu stron nierówności przez liczbę ujemną należy zmienić zwrot znaku nierówności.

Przykład 1.76

Rozwiązując nierówność 3x - 2<5x + 6, postępujemy analogicznie jakwpm-kładzie powyżej:

3x — 2 M 5x + 6,

3x -5x £6 + 2,

-2x <, 8 : (—2).

Stąd, pamiętając o zmianie zwrotu nierówności, mamy x > -4, a więc Równania i nierówności pierwszego stopnia z dwiema niewiadomymi

Definicja 1.67. Równanie postaci ax + by + c = 0, gdzie a, b, c są stałymi rzeczywistymi spełniającymi warunek a² + b² * 0, nazywamy równanie® liniowym (pierwszego stopnia) z dwiema niewiadomymi.

Rozwiązaniem równania ax + by + c = 0 są pary liczb (x_0f y₀) takie, że po ich podstawieniu do tego równania otrzymujemy zdanie prawdziwe. Obrazem feficznym (wykresem) zbioru rozwiązań równania pierwszego stopnia z dwie-Świadomymi jest prosta.

Przykład 1.77

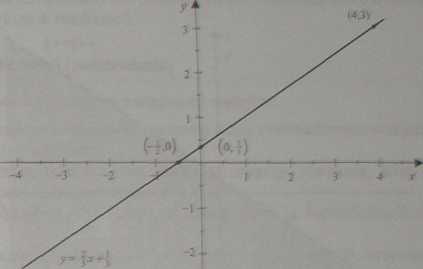
Równanie 2x - 3y + 1 = O ma nieskończenie wiele rozwiązań. Obrazem graficznym zbioru rozwiązań tego równania jest prosta o równaniu ogólnym 2x - 3y + 1 = 0. Przekształcając jej równanie do postaci kierunkowej, mamy y = fx+j;. Przykładowymi rozwiązaniami tego równania są pary. (4,3) (por. ilustracja 139).

Ilustracja 1.39. Zbiór rozwiązań równania 2x - 3y +1 —0

Definicja 1.681 Nierówności postaci; ax + by + c > Q, ax + by -* c < 0, ax + by + c £ 0, ax + by + c < 0. gdzie a, b. c są stałymi rzeczywistymi spełniającymi waruneka² + fr²* 0, nazywamy nierównościom pierwszego stopnia z dwiema niewiadomymi.

Obrazem graficznym zbioru rozwiązań nierówności liniowej pierwszego stopnia z dwiema niewiadomymi jest półpłaszczyzna o krawędzi określonej prostą ax + by+e =»0 (z tą prostą lub bez niej).