51732 PC043396

Przykład 1.56

Rozwiązując nierówność -*⁴ + 9t + 4r -12 > 0, szukamy najpierw | ■ równania -x* + 9r + 4* - 12 = 0. W tym celu będziemy postępowi gicznie jak w przykładzie 1.93, otrzymując rozwiązania x.\=b = -2.1

zaczynauoysmy oa góry). ramiętamy jeanoczesme^^Tjeśt pieiwiaj^ podwójnym, co oznacza, że w tym punkcie wykres nie przecina osi Ox,jJ się z nią styka (ilustracja 1.50).

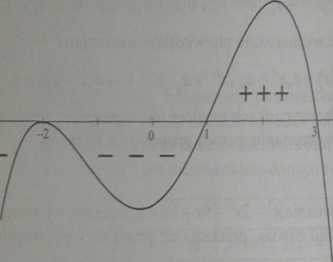
Z powyższego szkicu odczytujemy, że rozwiązaniem nierówności jest zk postaci {-2}u (13).

Ilustracja 1.50. Szkic wykresu funkcjiy=-x⁴+ftt²+4x -12

♦

1.6.4. Funkcja wymierna

Definicja 1.74. Funkcją wymierną zmiennej * nazywamy funkcję post**

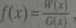
(1.1$

gdzie W i G są wielomianami oraz G nie jest wielomianem zerowym*^;i«j

Dziedziną funkcji wymiernej, określonej wzorem (1.12). jest zbiór tych liczb rzeczywistych, dla których G(x) * 0, czyli D,= {x e R: G(x) * 0}.

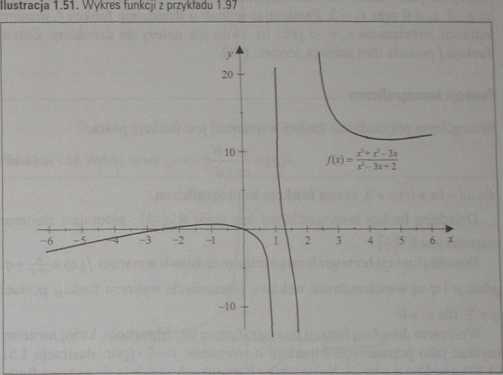
Przykład 1.97 Do dziedziny funkcji:

/(*)=

x³+x² -3x x²-3x²+2

(ilustracja 151), która jest przykładem funkcji wymiernej, należą wszystkie liczby rzeczywiste, dla których X² - 3x + 2 * 0. Wyznaczając pierwiastki trój-mianu X² - 3x + 2, otrzymujemy punktyx_x = 1 i x₂=2, dla których funkcja f jest nieokreślona, czyli D_f=R\{1,2}.

Na ogół do określenia własności funkcji wymiernych potrzebna jest znajomość rachunku różniczkowego (por. przykład 7.36). Jednak, podobnie jak to miało miejsce dla wielomianów, możliwe jest bezpośrednie wyznaczenie miejsc zerowych funkcji wymiernej.