prigogine20

DYLEMAT Epikuka

oraz trajektorie losowe, związane z rezonansami i wędrujące po całej przestrzeni fazowej. Teoria KAM opisuje, w jaki sposób topologia przestrzeni fazowej ulega przekształceniu w miarę wzrostu energii. Począwszy od pewnej wartości krytycznej, zachowanie układu staje się chaotyczne: wraz z upływem czasu sąsiednie trajektorie stają się rozbieżne. Kiedy chaos jest w pełni rozwinięty, możemy zaobserwować zjawiska dyfuzyjne i ewolucję ku równomiernemu rozproszeniu się po całej przestrzeni fazowej. Ale zjawiska dyfuzyjne są zjawiskami nieodwracalnymi: dyfuzja odpowiada zbliżaniu się do jednorodności w przyszłości i produkuje entropię. Jak zatem wytłumaczyć fakt, że, wychodząc z założeń dynamiki klasycznej, dochodzimy do ewolucji nieodwracalnej, czyłi łamiącej symetrię w czasie? Jak w ogóle wyrazić w języku dynamiki regularność, charakteryzującą zachowanie na poziomie statystycznym, w odróżnieniu od losowego, chaotycznego zachowania indywidualnych trąjektorii? Oto kluczowy problem, który trzeba rozwiązać, jeśli chcemy przezwyciężyć paradoks czasu.

Przede wszystkim należy wyodrębnić poziom indywidualny (trajektorie) i poziom statystyczny (zespoły), określony za pomocą rozkładu prawdopodobieństwa p. Rozbieżności spowodowane rezonansami odnoszą się do poziomu indywidualnego, podczas gdy na poziomie statystycznym mogą być one wyeliminowane (zob. rozdziały 5. i 6.). Jak pamiętamy, rezonanse prowadzą do sprzężenia między zdarzeniami (przypomnijmy chociażby sprzężenie dwóch dźwięków). Eliminacja rezonansów z poziomu statystycznego prowadzi do sformułowania teorii nie-newtonowskiej, nie dającej się pogodzić z opisem opartym na trajektoriach. Nie ma w tym nic dziwnego: rezonans i sprzężenie między zdarzeniami nie zachodzą w jednym punkcie i w jednej chwili.

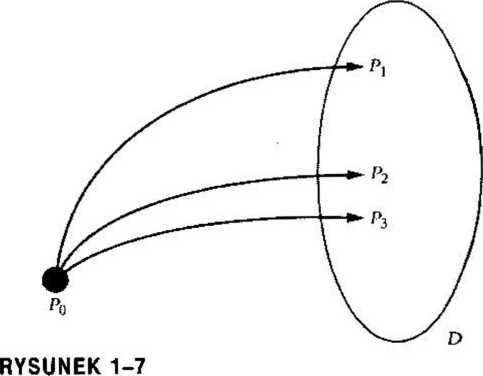
Ruch dyfuzyjny: po czasie t układ może znaleźć się w dowolnym punkcie Pi, P2, Ps obszaru D.

Wymagają one opisu nielokalnego, który nie daje się włączyć do ogólnie przyjętej dynamiki, bazującej na opisie pojedynczych punktów oraz trajektorii w przestrzeni fazowej. Rezonanse prowadzą do dyfuzji w przestrzeni fazowej. Jeśli początkowo układ znajduje się w punkcie P₀ przestrzeni fazowej, to nie możemy z całą pewnością przewidzieć, że po czasie t znajdzie się on w punkcie P_x. Możemy tylko określić obszar D, tak że dla każdego punktu, należącego do D, istnieje niezerowe prawdopodobieństwo znalezienia układu w tym punkcie po czasie x. Każdy punkt charakteryzuje się ściśle określonym prawdopodo-

59