prigogine12

DYLEMAT EPIKURA

nowym sformułowaniu nie dążymy do podania jednoznacznych i pewnych przewidywań, jak to było w przypadku praw deterministycznych, lecz rozważamy możliwości. Co więcej, to probabilistyczne ujęcie burzy symetrię czasu i pozwala tym samym, aby ewolucyjny charakter Wszechświata mógł wyrazić się w strukturze podstawowych praw fizycznych. Przypomnijmy w tym miejscu ideał zrozumienia zaproponowany przez Whiteheada (sekcja I): wszystkie elementy naszego doświadczenia mają zostać włączone w jeden spójny system pojęć ogólnych. Rozwijając zapoczątkowany przez Boltzmanna ponad sto lat temu program, fizyka posunęła się krok dalej na drodze do tego ideału.

lii

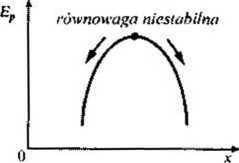
Różnica między układami stabilnymi i niestabilnymi jest znana. Rozpatrzmy przykład wahadła i przeanalizujmy jego ruch, uwzględniąjąc istnienie tarcia. Przypuśćmy najpierw, że w stanie równowagi wahadło jest nieruchome. Wiadomo, że jego energia potencjalna ma wówczas wartość minimalną. Po niewielkim wychyleniu następuje powrót do równowagi. Stan równowagi wahadła jest stanem stabilnym. Natomiast w przypadku ołówka — założywszy, że udałoby się ustawić go na czubku — równowaga jest niestabilna. Jakiekolwiek najmniejsze nawet zaburzenie powoduje przewrócenie się ołówka w jedną lub drugą stronę. Między układami stabilnymi i niestabilnymi istnieje zasadnicza różnica. W skrócie można powiedzieć, że stabilne układy dynamiczne to takie, w których niewielkie zmiany warunków po-

czątkowych nie pociągają za sobą większych skutków. Jednak dla pewnej bardzo licznej klasy układów dynamicznych konsekwencje takich zmian potęgują się wraz z upływem czasu. Skrajny przykład układu niestabilnego stanowią układy chaotyczne, ponieważ trajektorie odpowiadające dowolnie bliskim warunkom początkowym rozbiegają się tutaj w czasie w sposób wykładniczy. Mówi się wówczas o tak zwanej „wrażliwości na warunki początkowe”, co ilustruje znany „efekt motyla”: trzepot skrzydeł motyla w dorzeczu Amazonki wpływa na pogodę w Stanach Zjednoczonych.²³ Kilka przykładów układów chaotycznych przedstawię w rozdziałach 3. i 4.

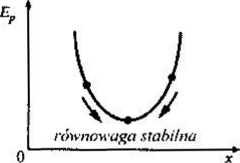
RYSUNEK 1-2

Często mówi się o tak zwanym „chaosie deterministycznym”. Istotnie, równania układów chaotycznych są równie deterministyczne, jak deterministyczne są prawa Newtona. A mimo to, opisują one zachowania o charakterze losowym! To zdumiewające odkrycie pozwoliło odnowić dynamikę klasyczną, uważaną do tej pory za zamknięty rozdział fizyki. Oznacza ono, że nie wszystkie układy opisane przez newtonowskie prawa są do siebie podobne.

43