70268 prigogine21

DYLEMAT EPIKURA

bieństwem przejścia. Dochodzimy tym samym, w kontekście czysto dynamicznym, do przedstawienia, które w uderzający wprost sposób przypomina dyfuzję towarzyszącą ruchom Browna. Najprostszy przykład ruchów Browna stanowi cząstka dokonująca w równych odstępach czasu przejścia o jedną jednostkę w jednowymiarowej sieci. W ruchu tym przy każdym przejściu przemieszczenie może nastąpić albo w prawo, albo w lewo, przy czym prawdopodobieństwo przejścia wynosi Vh. Oznacza to, że przy każdym przejściu przyszłość jest niepewna. A mimo to, na poziomie statystycznym, powyższy model pozwala uzyskać ściśle określone i regularne zachowanie, będące odpowiednikiem dyfuzji. Dyfuzja jest zjawiskiem ukierunkowanym w czasie: jeśli obierzemy za punkt wyjścia gęsty obłok punktów, po pewnym czasie obłok ten rozproszy się, przy czym niektóre punkty znąjdą się w pobliżu początku, inne zaś w znacznej odległości.

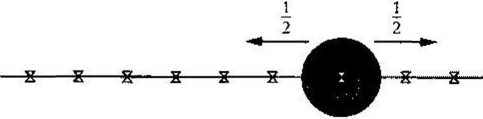
RYSUNEK 1-8

Ruchy Browna w jednowymiarowej sieci: przy każdym kroku prawdopodobieństwo przemieszczenia się cząstki w lewo lub w prawo wynosi ¹A.

Jest rzeczą godną uwagi, iż wychodząc od deterministycznych równań dynamiki klasycznej — a nie

od modelu ruchów Browna, w którym prawdopodobieństwa przejścia są dane — jesteśmy w stanie wykazać, że rezonanse wywołują pojawienie się wyrazów dyfuzyjnych. Na poziomie statystycznym rezonanse pociągają za sobą zerwanie z determinizmem, wprowadzają do mechaniki klasycznej niepewność i lamią symetrię czasową. W przypadku układu całkowalnego, wyrazy dyfuzyjne oczywiście nie istnieją i następuje powrót do opisu za pomocą trajektorii. Jest to jednak sytuacja szczególna: na ogół sformułowanie praw dynamiki musi uwzględniać prawdopodobieństwa. Przez całe wieki trajektorie uważane były za podstawowe obiekty dynamiki klasycznej: dzisiaj zakres ważności i stosowalność tego pojęcia okazują się ograniczone.

Pozostaje jednak pytanie zasadnicze: w jakiej sytuacji możemy się spodziewać pojawienia wyrazów dyfuzyjnych? Czyli — innymi słowy — jakie są granice stosowalności opisu newtonowskiego, opierającego się na trajektoriach, oraz opisu kwantowego, którego podstawowym pojęciem są funkcje falowe? Kwestie te rozwinę szczegółowo w rozdziale 5., w odniesieniu do mechaniki kwantowej zaś w rozdziale 6. Tutaj natomiast wskażę tylko, jakiego typu odpowiedzi można oczekiwać. W przypadku oddziaływań przejściowych (na przykład wiązka cząstek, która zderza się z obiektem, po czym kontynuuje ruch swobodny) wyrazy dyfuzyjne nie mają większego znaczenia. Pozostajemy wówczas w zasięgu newtonowskiej fizyki trajektorii. Z kolei, podczas oddziaływań długotrwałych (na przykład ciągły strumień cząstek padających na obiekt), dominujące stają się zjawiska dyfuzyjne. Oddziaływania przejś-

61