prigogine13

Dylemat Epikura

Oczywiście i dawniej wiedziano, że łatwiej obliczyć tor spadąjącego kamienia, niż ruch układu składającego się z trzech ciał (na przykład Słońca, Ziemi i Księżyca), lecz uważano, że jest to zwykły problem obliczeniowy. Dopiero pod koniec XtX wieku Poincare wykazał, że w zależności od tego, czy mamy do czynienia z układem dynamicznym stabilnym czy niestabilnym, zagadnienia, wobec jakich stajemy, okazują się diametralnie różne.²⁴ Problem trzech ciał należy już do kategorii układów niestabilnych. Trzeba było jednak doczekać ostatnich kilkudziesięciu lat, aby znaczenie odkrycia Poincarego zostało właściwie ocenione.

Wspominałem o układach chaotycznych, ale istnieją jeszcze inne rodząje niestabilności. Powrócimy do tego w dalszej części książki. Tutąj natomiast, z jakościowego punktu widzenia, chciałbym opisać drogę, jaka wiedzie od niestabilności do uogólnienia zasad dynamiki. Zacznymy od ogólnie przyjętych sformułowań. Stan początkowy przedstawiony jest za pomocą położeń q i prędkości v, lub pędów p (dla uproszczenia zapisu posługuję się tylko pojedynczym symbolem, nawet wtedy, gdy rozpatrywany układ składa się z dużej liczby cząstek, z których każda posiada określone położenie i określoną prędkość).

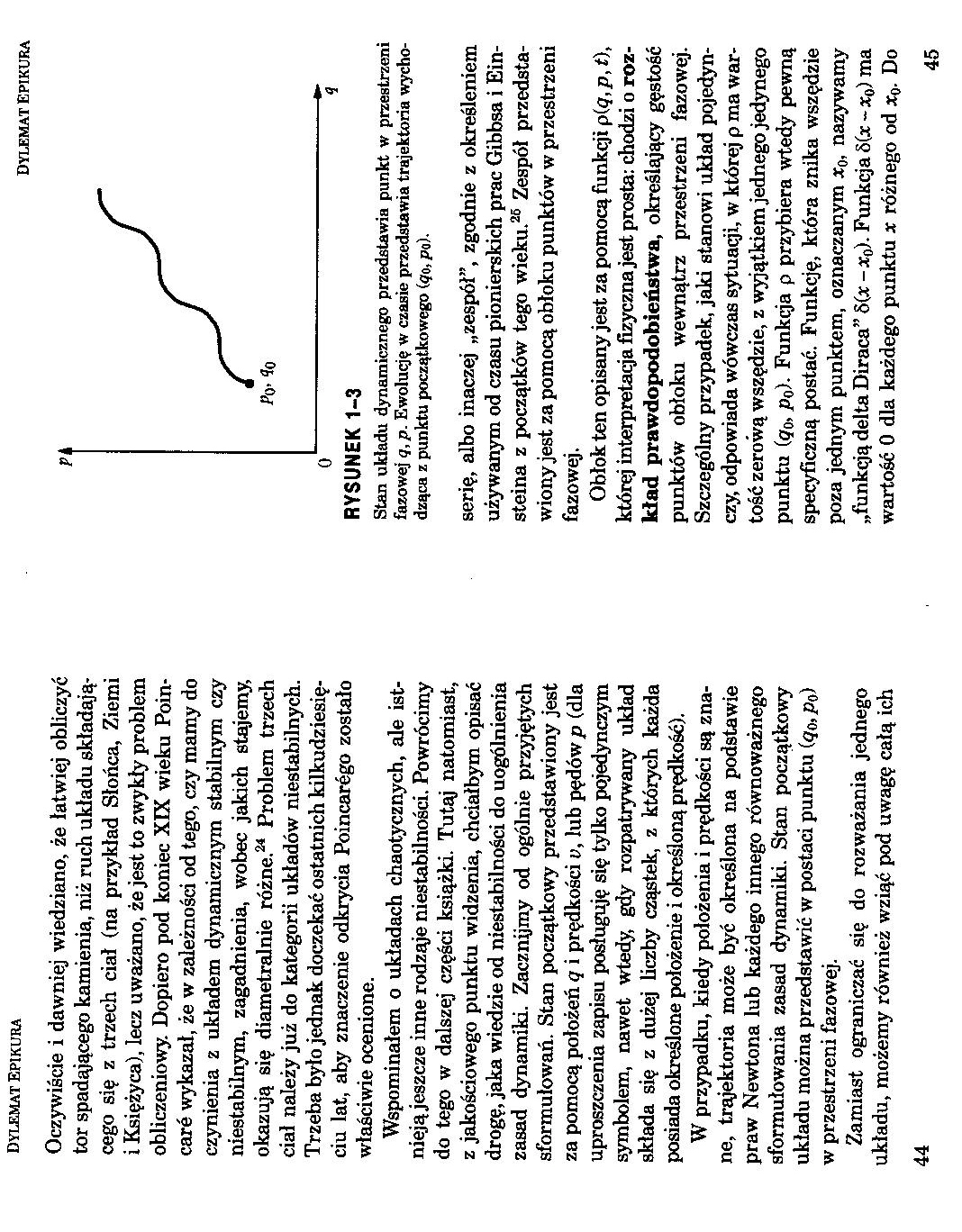
W przypadku, kiedy położenia i prędkości są znane, trajektoria może być określona na podstawie praw Newtona lub każdego innego równoważnego sformułowania zasad dynamiki. Stan początkowy układu można przedstawić w postaci punktu (qo,Po) w przestrzeni fazowej.

Zamiast ograniczać się do rozważania jednego układu, możemy również wziąć pod uwagę całą ich

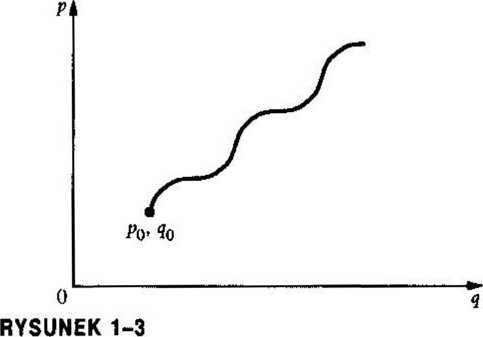
Stan układu dynamicznego przedstawia punkt w przestrzeni fazowej q, p. Ewolucję w czasie przedstawia trajektoria wychodząca z punktu początkowego (<70, po)-

serię, albo inaczej „zespół”, zgodnie z określeniem używanym od czasu pionierskich prac Gibbsa i Einsteina z początków tego wieku.²⁵ Zespół przedstawiony jest za pomocą obłoku punktów w przestrzeni fazowej.

Obłok ten opisany jest za pomocą funkcji p(q,p, t), której interpretacja fizyczna jest prosta: chodzi o rozkład prawdopodobieństwa, określający gęstość punktów obłoku wewnątrz przestrzeni fazowej. Szczególny przypadek, jaki stanowi układ pojedynczy, odpowiada wówczas sytuacji, w której p ma wartość zerową wszędzie, z wyjątkiem jednego jedynego punktu (<7q> Po)- Funkcja p przybiera wtedy pewną specyficzną postać. Funkcję, która znika wszędzie poza jednym punktem, oznaczanym r₀, nazywamy „funkcją delta Diraca” 5{* - x₀). Funkcja 5(x - x₀) ma wartość 0 dla każdego punktu x różnego od x₀. Do

45