74468 prigogine16

DYLEMAT EPIKURA

danego układu, to znaczy fakt, że jesteśmy w stanie przygotować tylko takie układy, w których rozkład prawdopodobieństwa koncentruje się na małym skończonym obszarze przestrzeni fazowej (ale nie takie, w których sytuacja początkowa daje się przedstawić za pomocą pojedynczego punktu) nie ma żadnych konsekwencji dla układów stabilnych. Natomiast dla układów niestabilnych, takich jak przedstawiony na rysunku 1-6, konsekwencją powyższego faktu jest niemożność takiego przygotowania układu, aby poruszał się on tylko wzdłuż trajektorii + lub trajektorii

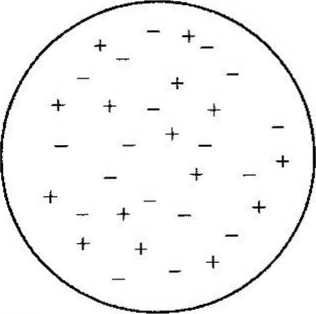
RYSUNEK 1-6

Niestabilny układ dynamiczny: każdy ruch + jest otoczony ruchami i na odwrót.

Czy trudność ta ma jedynie charakter praktyczny? Gdybyśmy mieli ograniczyć się stwierdzenia, że trajektorii takich nie da się policzyć, odpowiedź brzmiałaby: tak. Lecz chodzi o coś więcej: rozkład prawdopodobieństwa pozwala nam włączyć do opisu dynamicznego całą złożoną mikrostrukturę przestrzeni fazowej. Oznacza to, że zawiera on informację dodatkową, która ginie przy opisie pojedynczych trajektorii. Dochodzimy tu do zasadniczego punktu (do którego wrócimy jeszcze w rozdziale 4.): opis probabilistyczny okazuje się bogatszy od opisu indywidualnego, chociaż to przecież ten ostatni uważany byl zawsze za opis podstawowy. Dlatego właśnie możliwe jest uzyskanie na poziomie rozkładów prawdopodobieństwa p zupełnie nowego opisu dynamicznego, który pozwala przewidzieć ewolucję całego zespołu. Możemy w ten sposób otrzymać charakterystyczne skale czasu, odpowiadające zbliżaniu się funkcji rozkładu do stanu równowagi, co było niemożliwe w przypadku indywidualnych trajektorii. Równoważność między poziomem indywidualnym i poziomem statystycznym jest więc zburzona. W przypadku rozkładów prawdopodobieństwa dochodzimy do nowych rozwiązań, które są rozwiązaniami nieredukowalnymi, w tym sensie, że nie można ich zastosować do trajektorii indywidualnych. „Prawa chaosu”, związane z regularnym i mającym przewidywalny charakter opisem układów chaotycznych, pojawiają się na poziomie statystycznym. To właśnie miałem na myśli, mówiąc w poprzedniej sekcji o „uogólnieniu dynamiki”: chodzi nam o sformułowanie dynamiki na poziomie statystycznym, nie mające swego odpowiednika dla trajektorii. Prowadzi to do zupełnie nowej sytuacji — stanu początkowego nie można już określić, podając jeden punkt w przestrzeni fazowej; trzeba zdefiniować pewien obszar w tej przestrzeni, opisany za pomocą rozkładu prawdopodobieństwa. Jest to więc opis nielokalny. Co więcej, symetria czasu jest zła-

51