skan0083

86 Termodynamika chemiczna

AC_p(T) = a + bT+cT² = -\3J2 + 30,05 • 10~³ 7- 120,8 • 10~⁷ 7²,

a stąd, zgodnie z prawem Kirchhoffa (w postaci dostosowanej do arkusza kalkulacyjnego), mamy

AH°(T) =    AH°(T<)    - Ti (a + y T, + yr,²) + (a + y y T²]

albo, w zapisie skróconym, oznaczając wyrażenia w nawiasach jako H(7j) i H(7),

AH° (7) = [AH° (Jj) - Ti H (7))] + TH (7) = AH° (0) + TH (7),

gdzie, po podstawieniu wartości liczbowych, wyraz wolny AH° (0) = -280,14 • 10³ J • mol^-1.

Całkowanie relacji Gibbsa-Helmholtza w podanych granicach prowadzi do wyrażenia

AG°(T)

T

JG°(7₁)

T\

| |d//°(0) + T{a+%T + i T²) j _dT

AH°{ 0) . T_x

+ a ln Ti +

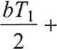
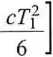
A (7j) - A (7),

^°(°),    , _rbT cT²1

-—--h a ln 7 + —— H--—

7    2    6

gdzie

AH°{0) _}rbT cT² v ' L 7    2    6 J

Podstawiając B = (dG°(7₁)/7_l +^(7^), możemy napisać AG°(T) = [B-A(T)]T, a stąd

AG° (7) = AH° (0) + BT- aT ln 7-4 7² - i 7³.

Po podstawieniu wartości liczbowych ^4 (7j) = 865,72 J • K^-1 • mol^-1, toteż B = 2,73 J • KT¹ • mol"¹.

Obliczenia, dla ułatwienia, były wykonywane za pomocą arkusza kalkulacyjnego - zob. tab. 3.6.

Tabela 3.6

AH°{ 0)	B	-a	-b/2	-cl 6
-280,14 • 10^3	2,730	13,72	-15,03 • nr^3	20,13 • 10~^7
7 [K]	H(T)	A{T)	zlG°(7)	formuła
298,15	-9,598	865,718	-2,573 • 10^5	-2,5730 • 10^5
1000	-2,722	198,376	-1,956 • 10^5	-1,9565 ■ 10^5