str (93)

CHAPTER IX

It will be remembered that Williamson introduced a two-term flow eąuation. Another empirical eąuation was introduced by Rabinowitsch, whichhe shows to be satisfactory for such materials as nitrocellulose in acetone, rubber in benzene, etc. His eąuation is

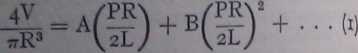
where A and B are constants. This is equivalent to

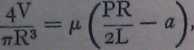
which is reminiscent of Bingham's treatment, except that the yield-value (a) is not a constant, but is proportional to the sąuare of the stress. This is a special case of a generał eąuation; but the theo-retical grounds are slender.

Eisenschitz has carried the idea further, and his ideas may be expressed somewhat as follows. When a flow curve shows upward curvilinearity, it does so because, at Iow stresses, strains cannot relax at a ratę comparable with the ratę of flow, whereas at high stresses, they relax faster. This implies a fali in viscosity as stress increases (structural viscosity).

9*

\lternatively one may say that it a shearing vnh _se a strain either in the compressible dispersed Hrticles or in some orientated structure ot aniso-tropie rigid partid.es, such that a rise in entropy is involved, the measured viscosity witt tah vńth increasing stress. It is proposcd that in place ot Maxwell's eąuation, we should write

T)V = S

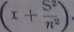
when v — the velocity gradient, n -- the rigidity modulus and S — stress. This is really the lirst part ot 1 series of even terms in S/rt, for which Hencky cl.tiras to fmd some theoretical basis. Moduli can only be dctcrmined indirectiy (from the relaxation times), and experimental yerification is difficuit.

In terms of t_r, the eąuation may be written

Eisenschitz’ ideas are probably the most highly developed that we have on the naturę of structural viscosity. He has applied them in practice to the study of cellulose esters.

Reiner proposes expanding the Newton eąuation into a Maclaurin series

For a capillary tubę his eąuation reduces to ¹

pR%₊no) i

6 YżL 7 ‘ 6

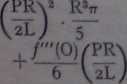
| The non-mathcmatical reader is reminded that /'(0)S means the first differential of S in respect to 5 at the point wbere v — O, f"(0)S is the second diflerential, and so forth.