wyzn,mac2 (6)

M) Elementy algebry liniowej

‘0	1	2		"0	1	1	0"
1	0	1	, B =	1	2	1	0
1	2	1		2	1	1	1

Odp. X =

5	5	1	1
4	4	2	4
1	1	0	1
2	2		2
1	3	1	1
4	4	2	4

14. Rozwiązać równania macierzowe

		"1	2	3'		5	0	10"		-	10	2	9'
a)	X	3	1	2	=	-5	5	-10	; Odp. X =		20	-3	-16
		1	2	4		0	0	-5			5	0	-5
	'1		2	f						T
b)	3		-1	2	X	= [4	4	nr	Odp. X =	i	J
	2		4	5						i

	c	"l	2	0'		'1	1	f	\		6		'-f
d)		2	1	1	+	2	4	1		X =	10	; Odp. X =	2
		1	0	1		2	-3	0			-7		2

§ 3. Układy równań liniowych

I. Rozwiązać układy równań stosując wzory Cramera

a)

Odp. x = 1, y = 1, z = 0;

2x-3y+ z = -l • x - y + z = 0 ; x + 2y-3z= 3

3x + 2y-3z = -l

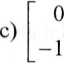
X

1    3

2    8

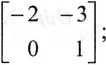
Odp. X =

^b)

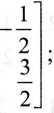
2x+ y-x + y+

z = 1 ; z- 4

Odp. x = 1, y = 1, z = 2;

O)

5x+ y-3z = 4 x y- z = 0; 2x + 2y+ z = l

3x-2y + z = 2 2x + y-z = 2 ; x — y+ z = 1

x + 2y-3z = 1 c) - 2x -5y+ z = 2; x + y + z = 1

x + 2y-3z+ u = -6 2x- y + 2z-2u= 5 -3x + 3y+ z + 2u = -2’ 2x-2y + 3z-3u = 3

Kozihiul 3

Odp.

O, y = 1, z = -

Odp. x = 1, y = 1, z = 1;

Odp. x = 1, y = O, z = 0;

Odp. x = 1, y = -l, z = 2, u = l

I >la jakich wartości parametru k układy równań są cramerowskie

«)

2x + ky + z = 0 • x - ky - 2z = 0 ; x + 2y + z = 0

Odp.

b)

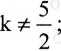
k² x + ky + z = 0 x + y + 2z = 0 2x+ y + 2z = 0

Odp. k ź —;

x + (k + l)y + z = 0

c) • 2x + (k-l)y + z = 0 ;    Odp. k^O.

2x-    y+z=0