img446

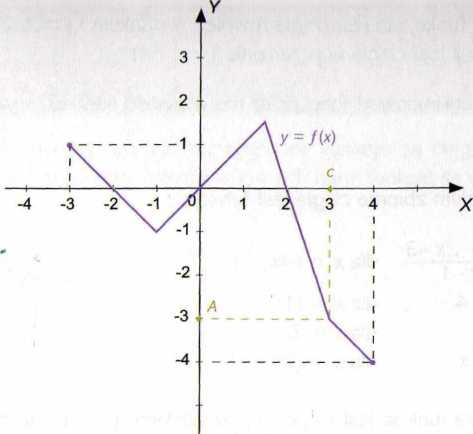
Funkcja ta jest ciągła w przedziale (-3, 4). Ponadto / (-3) = 1 oraz / (4) = -4, więc / (-3) * / (4). Niech A będzie dowolną liczbą taką, że -4 < A < 1. Wte dy w przedziale (-3, 4) istnieje (przynajmniej jedna) taka liczba c, dla której /(c) = A Jeśli na przykład A = O, to c = -2 lub c = O, lub c = 2; jeśli zaś A = -3, to c = 3 itd.

Spójrzmy teraz na funkcję g, której wykres jest następujący:

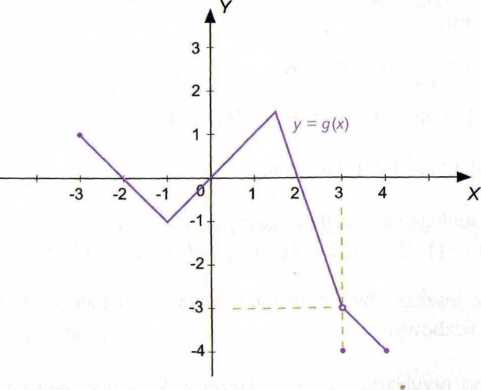
Ta funkcja zachowuje się już inaczej. Gdy weźmiemy A = -3, wówczas okazuje się, że nie istnieje takie c, by g(c) = A. Dzieje się tak dlatego, że funkcja ta nie jest ciągła w przedziale (-3, 4).

1

f ifnńwloną powyżej własność funkcji opisuje następujące twierdzenie.

tllZINI113. (własność Darboux)

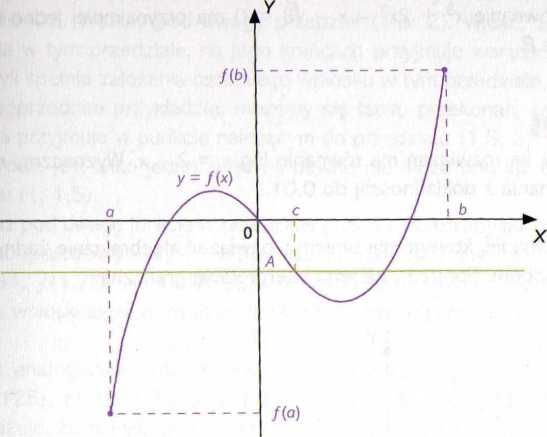
funkcja / jest ciągła w przedziale domkniętym (a, b) oraz /(o) * f(b), llast A jest dowolną liczbą pomiędzy liczbami /(a) oraz f(b), to istnieje Kba ce (a, b), dla której / (c) = A.

Jean Gaston Darboux [wym. ża gastą darbu] - matematyk francuski żyjący w latach 1842-1917. Był autorem prac poświęconych głównie geometrii różniczkowej i analizie matematycznej. Zajmował się też mechaniką teoretyczną.

» Dowód twierdzenia pomijamy.

i ł twierdzenia 1 3. łatwo jest wyprowadzić wniosek, który bywa wykorzystywany do przybliżonego rozwiązywania równań.

i WNIOSEK

Jeśli funkcja / jest ciągła w przedziale domkniętym (o, b) i f(a) ■ /(b) < O, to Istnieje taka liczba c e (a, b), dla której /(c) = O.

PRZYKtAO 24.

Wykażemy, że równanie x³ + 2x^z - x = 0 ma przynajmniej jedno rozwiązanie w zbiorze R.

i