0272

273

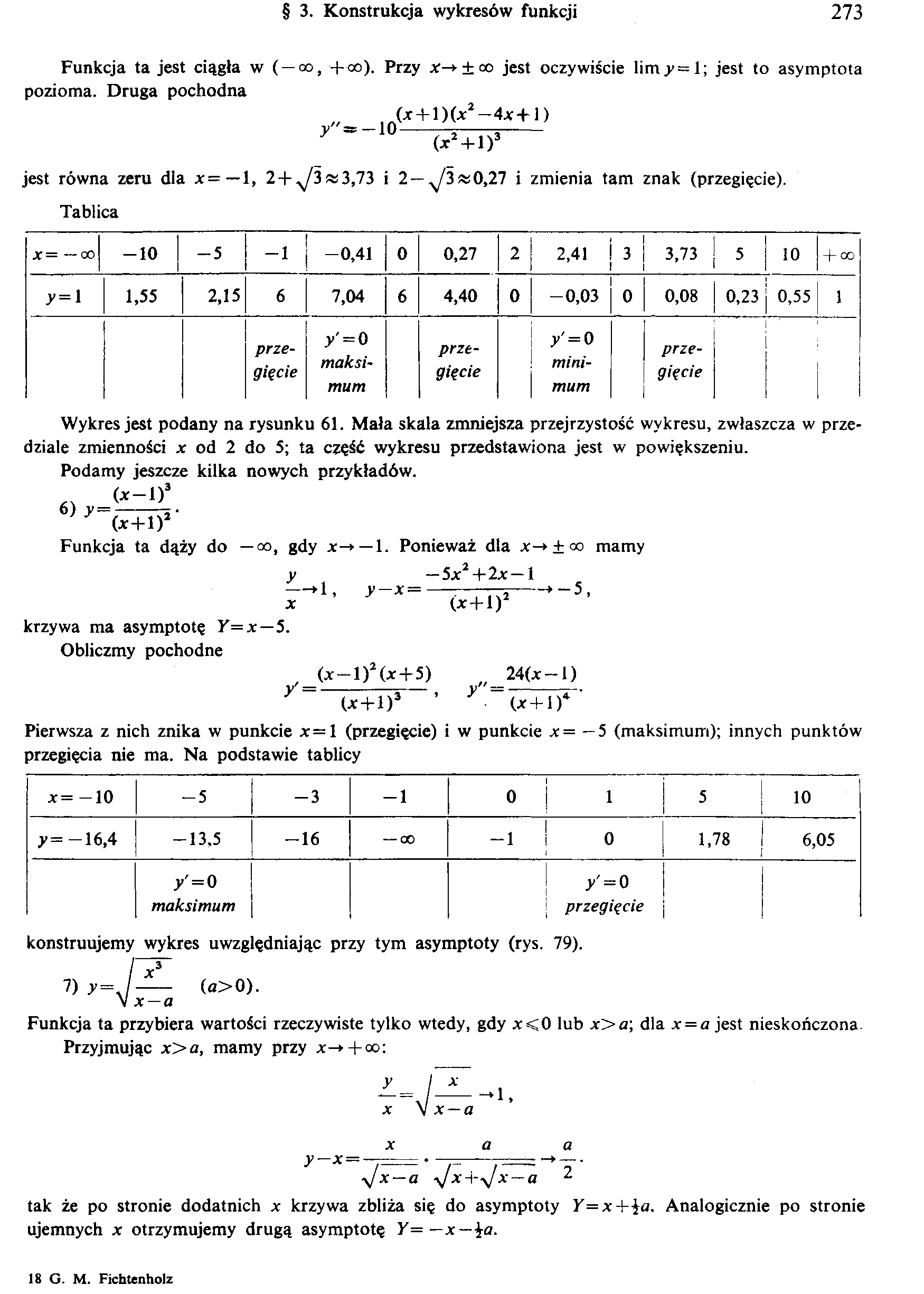
§ 3. Konstrukcja wykresów funkcji

Funkcja ta jest ciągła w ( — co, +co). Przy x-> ± co jest oczywiście limy=l; jest to asymptota pozioma. Druga pochodna

y"~-10

(jc + IM*-4*+l) (x² + l)³

jest równa zeru dla x=— 1, 2+^/3 as 3,73 i 2 — ^/3«0,27 i zmienia tam znak (przegięcie). Tablica

X = —00	-10	-5	-1	-0,41	0	0,27	2	2,41 i 3 1		3,73	5	10	+ OO
y=i	1,55	2,15	6	7,04	6	4,40	0	-0,03	0	0,08	0,23	0,55	1
			prze gięcie	/=o maksi mum		prze gięcie		y' = 0 minimum		prze gięcie		i j

Wykres jest podany na rysunku 61. Mała skala zmniejsza przejrzystość wykresu, zwłaszcza w przedziale zmienności z od 2 do 5; ta część wykresu przedstawiona jest w powiększeniu.

Podamy jeszcze kilka nowych przykładów.

(*-l)

Funkcja ta dąży do — oo, gdy x->— 1.

y .

-->1,    y—x=-

Ponieważ dla x-—5x²+2x — l

± co mamy

(*+ir

krzywa ma asymptotę Y= Obliczmy pochodne

x-5.

y=-

(x-1)²(x + 5) (X+1)³    ’

y -

24(jc — 1) (* + l)⁴ '

Pierwsza z nich znika w punkcie x—l (przegięcie) i w punkcie x = —5 (maksimum); innych punktów przegięcia nie ma. Na podstawie tablicy

x= —10	-5	-3	-1	0	i	5	10
y= -16,4	-13,5	-16	— 00	-1	0	1,78	6,05
	y' = 0 maksimum			/ = ° | | przegięcie j

79).

konstruujemy wykres uwzględniając przy tym asymptoty (rys.

7) y=J— («>0).

a jest nieskoóczona.

Funkcja ta przybiera wartości rzeczywiste tylko wtedy, gdy jc <0 lub x>a; dla x = Przyjmując x>a, mamy przy x->+oo:

y_

x

X

— -1,

x — a

x    aa

y—X = - . —₌---- —►

yjx — a yjx+yjx — a    ²

tak że po stronie dodatnich x krzywa zbliża się do asymptoty Y=x+%a. Analogicznie po stronie ujemnych x otrzymujemy drugą asymptotę Y= —x—±a.

18 G. M. Fichtenholz