44 (185)

2. FUNKCJE I ICH WŁASNOŚCI

2.4. WYBRANE PRZEKSZTAŁCENIA WYKRESU FUNKCJI

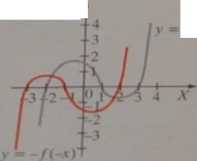
Dany jest wykres ftink-I I y -./'(.v) (lyc. obok): Omówione zostaną: l przekształcenie wykresu funkcji przez zmianę skali I przez symetrię względem osi układu.

Y		| y =/(v)
	-2
—3 j-2 -1.	0 -1	3-^3 4 x

2.4.1. Przekształcenie wykresu funkcji przez symetrię względem osi układu współrzędnych

a) Wykres funkcji y = /(—.v)jest obrazem wykresu funkcji y =/( .v ) w symetrii względem osi OY, na przykład:

Argumenty funkcji y=f(x)

iy = /(—,v) różnią się znakiem i punkty, których odcięte różnią się znakiem, leżą na płaszczyźnie symetrycznie względem osi OY. b) Wykres funkcji I

2.4.2. Przekształcenie wykresu funkcji przez zmianę skali (por. 6.3.2b.) Niech liczba k e /?₊ \{ i

Zmiana skali w stosunku k może dotyczyć: osi OX, osi OY lub osi OX i OY.

a) Wykres funkcji y = f(k x) jest obrazem wykresu funkcji y =f(x) w powinowactwie prostokątnym o osi OY i skali p na przykład:

y-/(2x) y =m . i

m

y =f(x)

y =-/(.v) jest obrazem wykresu funkcji y =/(.v) w symetrii względem osi OX, na przykład:

Wartości funkcji

y-f(x)

i y = — /( x) różnią się znakiem i punkty, których rzędne różnią się znakiem, leżą na płaszczyźnie symetrycznie względem osi OX. c) Wykres funkcji

y\

m

Uwaga: Nie zmieniają się rzuty prostokątne wszystkich trzech wykresów na oś OY.

Wykres funkcji y =f(x) ulega ^-krotnemu „ściśnięciu z lewa i z prawa” - jeśli k > 1 lub analogicznemu I „rozciągnięciu” w lewo i prawo — jeśli 0 < k < I. b) Wykres funkcji y = k ■/( x) jest obrazem wykresu funkcji y =f(x) w powinowactwie prostokątnym o osi OY i skali k, na przykład:

Uwaga: Nie zmie- i niają się rzuty pro- j stokątne wszystkich trzech wykresów na oś OX.

Jeśli k > 1 wykres funkcji y=/(x) ule- i ga A-krotnemu ..roz- j ciągnięciu w górę i w dół” lub „spłasz- : czeniu z góry i z dołu” - jeśli 0 < k < l. c) Wykres funkcji y = k₂ f(k, x) jest obrazem wykresu funkcji y=/(x) w obu przekształceniach zarazem (w złożeniu): w powinowactwie prostokątnym o osi OX i skali -r~ oraz w powi-nowactwic prostokątnym o osi OY oraz skali j

( (A,,A₂e/?₊\{i}) ) .

y=-f(-x) jest obrazem wykresu funkcji y =f(x) w symetrii względem początku układu współrzędnych 0(0; 0)

(czyli w złożeniu symetrii względem obu osi OX i OY). na przykład:

We wzorach y =f(x)iy    /(—x)zarówno argu

menty. jak i wartości funkcji różnią się znakami i punkty, których zarówno odcięte, jak i rzędne różnią się znakami, leżą na płaszczyźnie symetrycznie I I w górę i w względem początku układu współrzędnych.

na przykład:

Wykres funkcji y */( ,v ) ulega A,-krotncmu ściśnięciu (lub rozciągnięciu) w prawo i w lewo oraz A,-krotnemu rozciągnięciu (lub spłaszczeniu) dół.

2/(2* >

Y T
+4 |	ly
/*3 1	^1 /
J-JP I	/ ph
-3 U li
1 T ^5

O

i