36 (207)

V_)

2. FUNKCJE I ICH WŁASNOS

szą. Na wykresie ekstremum oznacza lokalnie najwyżej lub lokalnie najniżej położony punkt, czyli max

„wzniesienie”:    \ lub „zagłębienie”:    :

min

Wartość największa funkcji to maksimum globalne w całej dziedzinie lub w przedziale (a; 6). Graficznie wartości największej odpowiada najwyższy punkt wykresu funkcji.

Wartość najmniejsza funkcji to minimum globalne w całej dziedzinie lub w przedziale (a:6). Graficznie wartości najmniejszej odpowiada najniższy punkt wykresu funkcji.

Oto przykład wykresu funkcji, która ma ekstremum i nie ma ani wartości największej, ani najmniejszej w D_f=R:

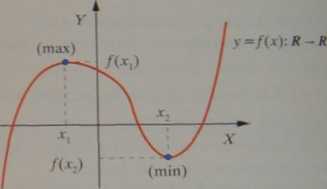
Funkcja ta osiąga w x, maksimum (lokalne) równe max/(x) =/(*,) oraz w x₂ minimum (lokalne) równe min/(.v) =/( x,).

Uwaga:

Funkcja ściśle monotoniczna w całej dziedzinie nie ma ekstremum.

Renć Descartes (Kartezjusz)

(1596-1650) - wielki filozof, pionier nowoczesnej matematyki, który zajmował się również optyką, chemią, mechaniką, anatomią, embriologią, medycyną, astronomią. Urodził się we Francji.

Kartezjusz głosił racjonalistyczne idee o potędze rozumu ludzkiego i z tego względu spotkał się z prześladowaniem ze strony Kościoła katolickiego. Dlatego też, chcąc znaleźć odpowiednie warunki umożliwiające mu pracę naukową (a jego zainteresowania filozofią i matematyką datowały się już od wczesnych czasów szkolnych), osiedlił się w 1629 roku w Holandii, gdzie spędził prawic całą resztę swego życia.

2. Funkcje i Ich włnsnoici

2.1.6. Interpretacja graficzna podstawowych własności funkcji (por. 2.5.2.)

I a) Dziedzina i zbiór wartości (por. 2.5.2a.)

Dziedzina D_f jest to prostokątny rzut wykresu (..prostopadły cień") na oś OX, zbiór wartości Y_w

-    analogicznie - na oś OY.

J b) Miejsca zerowe (por. 2.l.5a. i 2.5.2b.)

Zgodnie z definicją - x₀ jest miejscem zerowym, gdy f{x₀) = 0, zatem graficznie odpowiada mu punkt (.v_o;0). Miejsc zerowych funkcji szukamy w punktach przecięcia jej wykresu z osią OX.

c)    Znaki funkcji (por. 2.1.Sb. i 2.5.2c.)

Uwaga: W matematyce są dwa znaki:

+ - znak dodatni oraz

-    - znak ujemny.

Wyrażenie: „znak funkcji” oznacza: „znak wartości funkcji”.

Graficznym odpowiednikiem nierówności: f(x)> 0 jest fragment wykresu znajdujący się nad osią OX (w górnej pólpłaszczyinie), f(x)< 0 jest fragment wykresu znajdujący się pod osią OX (w dolnej pólplaszczyźnie).

d)    Monotoniczność funkcji (por. 2.1.5c. i 2.5.2f.)

Symbol funkcji monofonicznej oznacza ułożenie jej wykresu:

rosnącej / - kierunek: od lewego dolnego do prawego górnego

malejącej \ - kierunek: od lewego górnego do prawego dolnego

e)    Ekstremum, wartość największa i najmniejsza (por. 2.1.5d. i 2.5.2h.)

Ekstremum (maksimum i minimum) to własność lokalna. Maksimum oznacza lokalnie wartość największą, zaś minimum - lokalnie wartość najmniej-

---------- ■ ■ ■ - -    ^r—|

W jednym ze swych listów Kartezjusz wyraża

w następujący sposób swoje zadowolenie z pobytu w Holandii: „Tu każdy oprócz mnie jest tak zajęty swymi interesami i dochodami, że mógłbym przeżyć cale życie, nie będąc zauważonym przez kogokolwiek... W którym innym kraju można cieszyć się taką wolnością, gdzież można by spać z większym spokojem niż tu, gdzie trucizna, zdrada, oszczer- j stwo są znacznie mniej znane...”.

W Holandii Kartezjusz napisał wszystkie swoje wielkie prace z dziedziny filozofii, matematyki, fi-zyki, kosmologii i fizjologii.

Swój dorobek w dziedzinie matematyki zebrał w jednym dziele Geometria (1637). Przedstawił w nim podstawy geometrii analitycznej i algebiy ! Po raz pierwszy wprowadził pojęcia: zmiennej, funkcji oraz współrzędnych prostokątnych, które do dziś nazywamy współrzędnymi kuric/janskinu