0270

271

§ 3. Konstrukcja wykresów funkcji

Przypuśćmy teraz, że krzywa y=f(x) ma asymptotę pochyłą (2)    Y = ax + b

(rys. 78), powiedzmy po dodatniej stronie osi x. Ponieważ różnica rzędnych \y— Y| różni się od odległości 8 tylko stałym czynnikiem (który równa się kosinusowi kąta między

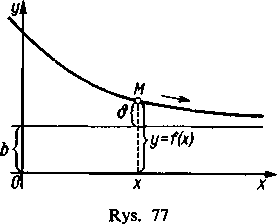
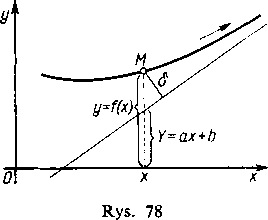
asymptotą a osią x), więc gdy *-► + co, jednocześnie z 8 dąży do zera także ta różnica

(3)    lim (y — ax — b)=0.

+ 00

Dzieląc przez x otrzymujemy stąd

(4)    lim —==a ;

jc^-► + oo X

oprócz tego równość (3) daje bezpośrednio

lim (y-ax) = b.

W/    x-* + oo

Tak więc na to, by prosta (2) była asymptotą danej krzywej, potrzeba, by spełnione były warunki (4) i (5). Odwrotne rozumowanie pokaże nam łatwo, że warunki te są również dostateczne. Zagadnienie sprowadziło się tu do kolejnego obliczania granic (4) i (5), które wyznaczają nam już współczynniki równania prostej (2).

Dla x-> — oo trzeba rzecz jasna powtórzyć całe badanie.

W przypadku hiperboli (1), biorąc na przykład jc-+ + oo, mamy

y    b    \!x²-a²    b I a²    b

— =±— ’--=± —_x/l--2    — ,

x    a x    a    v x    a

b _ b /    j . _    ab

y T —*= + —W x²-a²-x)= +-7===-

^{a    a}    x + vx² — a²

dochodzimy do znanych nam już asymptot

b

y= ± — x. a