Monotoniczność funkcji (3)

3

Stąd funkcja y(x) = x + — jest:

x

-    rosnąca w przedziałach (-00, -1) oraz (1, + 00)

-    malejąca w przedziałach (-1, 0) oraz (0,1)

Punkt x = 0 nie należy do obszaru określoności funkcji y(x) = x + —.

x

Zadanie 3. Zbadać monotoniczność funkcji y(x) = —r-.

x~ +1

Rozwiązanie. Funkcja y jest określona na całej osi liczbowej R i jest różniczkowalna. Pochodna y jest równa

_ d x _ 1 ■ (x² +1) - x • 2x _ l-x² _ (1 -x)(l + x) ^y{X’~~dxx²+1 “    (x²+l)²    ~(x²+l)^2_    (x²+l)²

Znak wyrażenia ^    ^zal^eży °d znaku licznika, gdyż mianownik jest większy od zera

w każdym punkcie osi liczbowej R.

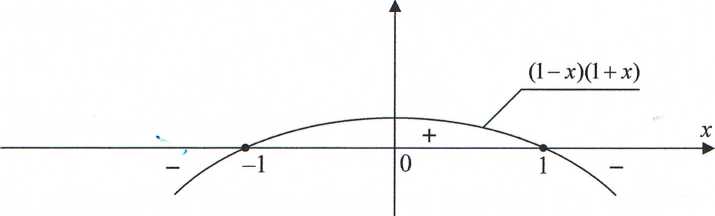
Wyrażenie (1 - x)(l + x) określa parabolę, która jest równa zeru w punktach x = -1, x = 1. Wykres paraboli (l-x)(l + x) pokazany jest na rysunku

X

Stąd funkcja y(x) = —₅-jest:

x +1

-    rosnąca w przedziale (-1,1)

-    malejąca w przedziałach (-00,-1) oraz (1,+ 00)