MATEMATYKA181

352 Vn Macierze. Wyznaczniki. Układy rówtian liniowych

Tak więc, aby obliczyć wyznacznik przekształcamy go najpierw do takiej postaci, aby w pewnym wierszu (kolumnie) wystąpiło maksymalnie dużo zer, a następnie rozwijamy otrzymany wyznacznik według lego wiersza (kolumny), Obliczmy tą metodą wyznacznik:

2 -1	2	-1		2	1	-2	-3
1 -1	2	1	fw dmgim wierszu tworzymy zera 1	1	0	0	0
-2 3	-1	1	[pr/y pomocy pierwszej kolumny J	-2	1	3	3
1 -2	1	1		1	-1	1	0

rozwijamy wyznacznik według 2 - ego wiersza

	1 -2	-3		1	-3	-3
}—	1 3	3	2? —	1	2	3
J	-1 -1	0		-1	0	0

rozwijamy wyzi łącznik 11-3 -3 według 3-ego wiersza j 2    3

2) Metoda Chio, czyli metoda obniżania stopnia wynika wprost z własności (8): po lewej stronic wzoru znajduje się wyznacznik n-tego stopnia, a po prawej - wyznacznik stopnia n-1, ale elementy b_lk tego wyznacznika są również wyznacznikami. Metoda jest bardzo efektywna pod warunkiem, że nauczymy się, co nic jest wcale trudne, sprawnie obliczać elementy bj_k. Na przykład

2 -1 1 -1

-2    3

I -2

2

2

-I

ł

-12 3 4 2 O

-3 O 3

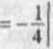
-10

6

-12

6

*= -3.

MACIERZ ODWROTNA Macierzą odwrotną do macierzy' A nazywamy taką macierz A ¹ (o ile istnieje), dla której

AA"¹ = A ¹A = I,

gdzie I oznacza macierz jednostkową,

7. definicji tej wynika, że macierz odwTotna może istnieć jedynie dla macierzy kwadratowej. Wykazuje się, że macierz odwrotna istnieje dla każdej macierzy kwadratowej, której wyznacznik jest różny od zera

TWIERDZENIE 1.1 Jeżeli A jest macierzą kwadratową, której wyznacznik jest różny od zera, czyli detA = W*0, to istnieje dokładnie jedna macierz odwrotna do macierzy A i jest ona określona wzorem:

W

Uwaga. Macierz A, dla której dctA*0 nazywamy macierzą nieosobliwą.

PRZYKŁAD 1.3 macierzy

Znajdziemy macierz odwrotną do

A =

2 -1 1 1 0 1 0 2 t

Obliczamy wyznacznik tej macierzy stosując metodę obniżania stopnia:

det A = W =

2 -1 1 1 0 1

0 2 1

1 1 4 2

Ponieważ W = -1 * 0, więc istnieje macierz odwrotna do macierzy A. Budujemy kolejno macierze:

[W*]

Wu	W|2	w,3”		-2	1	2
w2,	W22	W23	=	-3 -1	2 I	4 I
[W,,	W32	^W33,

Przypomnijmy: W_lV jest to podwyznacznik otrzymany z wyznacznika W przez pominięcie i-tego wiersza oraz k-tej kolumny. Ponieważ W* =(-l)”^kW_lk, więc

Kl=	-2 -i 2
	3 2 -4
1	-1 -1 1

w?_Ł

2 I -2 -3 -2    4

1 1 -1

Następnie tworzymy macierz

W

oraz macierz transponowaną do niej. Otrzymana macierz jest macierzą odwTotną do macierz)' A: