new 64

130

7. Zasady obliczeń wytrzymałościowych śrub

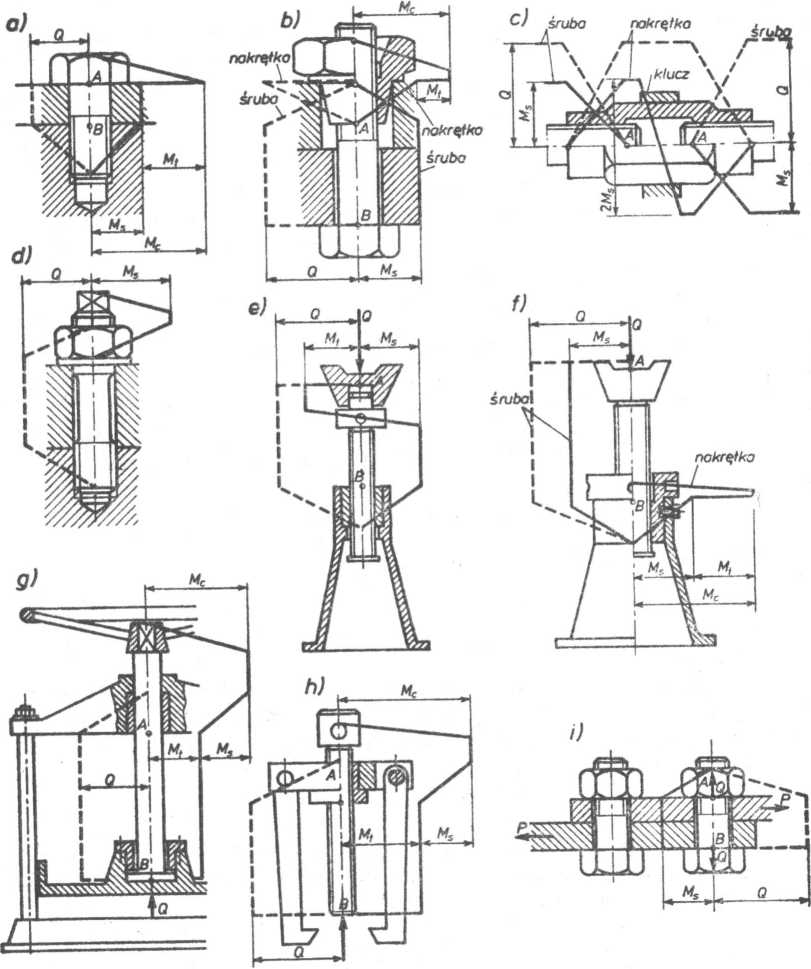
Rys. 7.11. Schematyczne przykłady połączeń gwintowych, w których śruby przenoszą obciążenia osiowe Q i momenty skręcające M

7.3. Obliczenia śrub rozciąganych i skręcanych

131

Na rysunku 7.11 przedstawiono kilka przykładów połączeń gwintowych z uwzględnieniem rozkładów obciążeń osiowych (rozciągających lub ściskających) oraz (momentów skręcających M. Złożony stan obciążenia w przedstawionych przykładach nie występuje na całej długości śruby, a tylko na odcinkach AB. Moment wywołujący skręcanie śruby może wynikać z oporów ruchu na gwincie lub z tarcia na powierzchni oporowej śruby lub nakrętki. Moment oporów ruchu gwintu M, określony jest wzorem (4.12), a moment tarcia M_t wzorem (4.14). Śruba na odcinkach przenoszących pełne obciążenie osiowe Q w przypadkach przedstawionych na rys. 7.11a-Pf jest skręcana momentem M = M_s, a w przypadkach zilustrowanych na rys. 7.lig, h ■— momentem M — M_t. Znacznie większemu skręcaniu podlegają śruby z gwintami pasowanymi ciasno. Moment oporów ruchu takich śrub zależy nie tylko od wymiarów gwintu, materiału łączników i gładkości powierzchni roboczych, ale przede wszystkim od wielkości wcisku skutecznego w. Pod pojęciem wcisku skutecznego rozumie się sumę odkształceń sprężystych śruby i nakrętki na średniej średnicy gwintu d_s po dokonaniu połączenia.

Wcisk skuteczny w jest mniejszy od wcisku nominalnego (zmierzonego) W, oznaczającego różnicę średnich średnic gwintu śruby i nakrętki przed skręceniem. W procesie skręcania następuje bowiem deformacja plastyczna i częściowe starcie wierzchołków nierówności na powierzchni styku. Między wspomnianymi wielkościami istnieje zależność

(7.14)

u> = W-l,2(R_a + R₂₂),

gdzie R_2ł, R-2 są wysokościami chropowatości profilu zarysu gwintu zewnętrznego i wewnętrznego.

Przy średniodokładnym wykonaniu gwintów R_z = 6-P16 pm, przy dokładnym R_z = 2,5-1-6 pm.

Dla uproszczenia schematu obliczeń przyjmuje się, że śruba przedstawiająca sobą gładki walec o średnicy d„ jest wciśnięta w wydrążony walec o wewnętrznej średnicy d_s i zewnętrznej średnicy D.

Z rozwiązania zadania rur grubościennyeh wynika zależność

(7.15)

gdzi£ Po — jest naciskiem promieniowym na umownej cylindrycznej po-

wierzchni gwintu (patrz rys. 7.12), i v₂ są współczynnikami Poissona materiału śruby i nakrętki (lub nagwintowanego korpusu), a E_x i E₂ — modułami sprężystości podłużnej materiału śruby i nakrętki. Przekształcenie wzoru (7.15) ze względu na p₀ daje

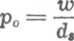
1

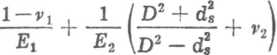
(7.16)