62185 skan0131

134 Roztwory i równowagi fazowe

Zależność między aktywnością rozpuszczalnika aj a aktywnością substancji rozpuszczonej a₂ określa równanie Gibbsa-Duhema

X\d\na\ + x₂d\na₂ - 0,    (4.15)

zgodnie z którym aktywności składników nie mogą zmieniać się w sposób niezależny. Jeżeli znana jest aktywność jednego z nich jako funkcja składu oraz aktywność drugiego dla jakiegoś jednego stężenia, to całkując to równanie można obliczyć aktywność drugiego składnika dla innych stężeń.

Przykład 4.5. Badając w 50°C prężność i skład par¹ nad mieszaniną 1,4-^dioksanu (1) i chloroformu (2) uzyskano poniższe wartości aktywności 1,4-dioksanu:

*1	0,8	0,7374	0,6385	0,525	0,4445	0,3282	0,122
“1	0,795	0,727	0,603	0,462	0,358	0,230	0,054

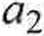
Obliczyć aktywność chloroformu a₂ w mieszaninie o x] = 0,122, wiedząc, że w mieszaninie o X\ = 0,8 wynosi 0,106.

Rozwiązanie. Przekształcając równanie Gibbsa-Duhema (4.15): 'Lx_idln a_t = = 0, do postaci

x₂ d ln a₂ = - Xj d ln a \,

otrzymujemy równanie całkowe

b    ^B x

<71ncb=- —~ d\na\,

^{J    J} To

A    A

gdzie A oznacza = 0,8 (odpowiada mu a₂ - 0,106) natomiast B oznacza = = 0,122. Rozwiązanie tego równania ma postać

B

ln (a₂)_B = ln (a₂)_A -J —^L dlna^

A *2

Na podstawie danych zawartych w tab. 4.3 wykreślamy funkcję podcałkową x\lx₂ w zależności od ln a_x (rys. 4.3). Znaleziona metodą trapezów (zob. przykład 3.16, s. 76), wartość całki w tych granicach wynosi ZR, = -2,0972. Po podstawieniu tej liczby do równania na aktywność otrzymamy ln(a₂)/; ⁼ ln0,106 -- (-2,0972) = -0,1471; (a₂)_B = 0,863.

Porównując ją z wyznaczoną doświadczalnie aktywnością chloroformu (a₂ = = 0,858), w mieszaninie o tym składzie, możemy uznać zgodność za bardzo dobrą. Jest to zarazem sprawdzian poprawności zarówno pomiarów, jak i obliczeń wszystkich wartości a_](x₁).

1

H. Buchowski, W. Ufnalski, Roztwory, WNT, Warszawa 1995, s. 69.