CCF20091202029

r

Gdyby liczebności tych społeczności były równe, moglibyśmy za średnią ogólną przyjąć zwykłą średnią z tych trzech średnich dochodów. Ale społeczność A jest dwukrotnie większa od B; innymi słowy liczba 3518 doi. reprezentuje dwukrotnie większą liczbę przypadków niż liczba 4760 doi. Gdybyśmy potraktowali wszystkie 23000 osób jako jedną próbę i obliczyli średni dochód bez dzielenia ich na społeczności, fakt ten zostałby uwzględniony. Możemy jednak otrzymać prawidłową wartość średniej w inny sposób: ważąc każdą z trzech średnich liczbą przypadków jej odpowiadającą. Następnie zaś sumujemy iloczyny i dzielimy tę sumę przez całkowitą liczbę przypadków (23000). Otrzymujemy:

k

Yj Nt X_t

x= ^,r'-_N    (5.8)

gdzie N, i X_t są odpowiednio liczbą przypadków i średnią i-tej kategorii, k zaś jest liczbą kategorii. Tak więc

10000 (3518)+ 5000 (4760)[phone])

^—    23000

3998,09 doi.

91 956000 23000

Procedurę tę łatwo uzasadnić: średnia /'-tej kategorii jest przecież sumą pomiarów podzieloną przez N_t. Iloczyn N,X_t jest więc sumą pomiarów zawartych w /-tej kategorii. Dodając te iloczyny otrzymujemy sumę wszystkich pomiarów, a dzielenie jej przez N daje średnią ogólną, to znaczy ten sam wynik jaki otrzymałoby się przy pominięciu kategorii. Ważenie średnich jest metodą bardzo przydatną. Łatwo zauważyć, że podobne postępowanie w przypadku mediany nie jest możliwe. Znając wartości środkowych pomiarów w kilku oddzielnych kategoriach nie potrafimy obliczyć wartości środkowego pomiaru po połączeniu tych kategorii.

Jeszcze kilka słów o ostatniej ważnej różnicy między średnią i medianą. Obliczanie średniej wymaga skali interwałowej. Gdy pomiar jest słabszy, nie ma sensu mówić o dodawaniu pomiarów. Jest oczywiste, że suma liczb 30 i 45 powinna być równoważna sumie liczb 20 i 55, gdyż obie pary mają tę samą średnią. Natomiast medianą można posługiwać się nie tylko przy skalach interwałowych, lecz i przy porządkowych. Dla tej ostatniej skali wartość liczbowa mediany nie ma oczywiście znaczenia, ważne jest jednak zlokalizowanie środkowego pomiaru. Oznaczą to m. in., że możemy podzielić pomiary na dwie kategorie: pomiary poniżej i powyżej mediany. Mierników pozycyjnych można więc używać przy skalach porządkowych: jest to fakt bardzo pomocny przy opracowywaniu testów nie wymagających skali interwałowej.

5.5. INNE MIARY TENDENCJI CENTRALNEJ

Istnieje jeszcze kilka innych mierników tendencji centralnej, żaden z nich jednak nie znalazł szerszego zastosowania przy opracowywaniu danych socjologicznych. Jednym z nich jest wartość modalna, czyli przypadek najczęstszy. Przyjrzymy się następującym seriom pomiarów:

(1)    71,    75, 83, 75,    61,    68

(2)    71,    75, 83, 74,    61,    68

(3)    71,    75, 83, 75,    83,    68

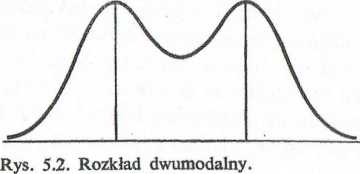
Pierwsza ma wartość modalną 75, gdyż ta wartość — i żadna inna — pojawia się w serii dwukrotnie. Seria druga nie ma wartości modalnej, trzecia zaś ma dwie wartości modalne (75 i 83). Wartość modalna może być miernikiem użytecznym, gdy pomiarów jest więcej i gdy są one pogrupowane. Mówimy czasem o przedziale modalnym, a środek tego przedziału klasowego uznajemy za wartość modalną. Dla danych, które analizowaliśmy w tym rozdziale, przedziałem modalnym był przedział 5000-5900. W rozkładzie liczebności wartość modalną wskazuje najwyższy punkt krzywej. Gdy rozkład jest symetryczny i ma tylko jedną wartość modalną w środku, średnia mediana i wartość modalna leżą w tym samym punkcie. Istnieją jednak rozkłady „jednomodalne” i „dwumodalne” — jak np. rozkład na rys. 5.2. W tych ostatnich — wbrew definicji wartości modalnej i rysunkowi 5.2. wysokości obu wierzchołków nie muszą być sobie równe. Zauważmy też, że ponieważ wartość modalna odnosi się do kategorii

75