85213 str265

ROZDZIAŁ 5

Zarys rachunku tensorowego

§ 1. Pojęcie tensora

Definicja 1. Przestrzenią abstrakcyjną nazywamy zbiór, w którym zostało określone pojęcie granicy ciągu elementów tego zbioru.

Definicja 2. Przestrzenią metryczną nazywamy zbiór X, jeżeli każdej parze a, b jego elementów odpowiada liczba rzeczywista nieujemna g(a,b), spełniająca następujące warunki:

1.    g(a, b) = 0, wtedy i tylko wtedy, gdy a = b (aksjomat tożsamości),

2.    g(a, b) = g(b, a) (aksjomat symetrii),

3.    g(a, b)+g(b, c)^g(a, c), gdzie c jest również elementem zbioru X (aksjomat trójkąta).

Liczbę Q(a, b) o podanych w definicji 2 własnościach nazywamy odległością punktów a i b, a wymienione trzy warunki nazywamy aksjomatami metryki przestrzeni X.

Szczególnym przypadkiem przestrzeni metrycznej jest znana nam z podstawowego kursu wyższej matematyki przestrzeń Euklidesa. Sformułujemy dla przypomnienia definicję tej przestrzeni.

Definicja 3. Przestrzenią Euklidesa A-wymiarową nazywamy zbiór X wszystkich uporządkowanych układów A liczb rzeczywistych, jeżeli odległość pomiędzy dwoma dowolnymi punktami a, be X, gdzie a — {{j,    ..., £_w} i b = {>/,, t/₂, ..., ą_N} , określona

jest wzorem:

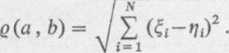
(1.1)

Można sprawdzić, że odległość g podana wzorem (1.1) spełnia aksjomaty metryki. W praktycznych zagadnieniach najczęściej mieliśmy do czynienia z przestrzeniami Euklidesa dwu- lub trójwymiarowymi oznaczonymi zazwyczaj symbolami

/

E² lub E³.

Pojęcie tensora będziemy wiązać z przestrzeniami metrycznymi, przy czym w przypadkach szczególnych z A-wymiarową przestrzenią Euklidesa, a w bardziej ogólnych przypadkach z przestrzenią Riemanna. Definicja tej przestrzeni będzie podana w § 3.