Zofia Krawczyk

III WF - grupa 1 ż.

POMIAR PRĘDKOŚCI RUCHU W FUNKCJI MOMENTU SIŁY OBCIĄŻAJĄCEJ STAW

WPROWADZENIE

Ważnym zadaniem i przedmiotem badań biomechaników, a jednocześnie cenną informacją dla trenera, jest określenie zależności pomiędzy prędkością a siłą rozwijaną przez zawodnika podczas wykonywania dowolnych ruchów. W sporcie można popełnić błąd oceniając oddzielnie te dwie cechy. Zależnością pomiędzy rozwijaną prędkością a siłą obciążającą mięsień zajmował się A.V.Hill. Badania przeprowadzał dla mięśnia izolowanego. Model takiego zjawiska Hill przedstawił w postaci równania:

( F + a ) v = b ( Fmax - F )

gdzie: F , Fmax - odpowiednio bieżąca i maksymalna wartość siły,

v - prędkość skracania się mięśnia,

a , b - stałe współczynniki.

Istotną cechą tego modelu jest fakt, że mięsień rozwija stałą moc. Równanie to charakteryzuje wykres zwany krzywą Hilla:

Z równania Hilla wynika, że przy skurczu izotonicznym prędkość skracania się mięśnia zmniejsza się hiperbolicznie wraz ze wzrostem obciążenia. Uzyskuje się hiperbolę o asymptotach równych stałym a i b .

Właściwość ta, została potwierdzona przez wielu autorów, którzy badali zależność v = f (F), która została zmodyfikowana ω = f (M) dla zespołu mięśni prostowników stawu kolanowego. Pomiar zależności prędkości kątowej (ω) od wartości momentu obciążającej staw (M) pozwala nam określić moc jaką rozwija dana osoba. Dla ruchów obrotowych moc jest równa:

P = M ω

gdzie: M - moment siły wywołujący ruch,

ω - prędkość kątowa ruchu.

CEL BADANIA

Celem badania jest wyznaczenie charakterystyk biomechanicznych pojedynczy zespołów mięśniowych (prostowników stawu kolanowego) w warunkach dynamicznych polegających na:

• pomiarze prędkości kątowej w funkcji zewnętrznego obciążenia,

• pomiarze mocy rozwijanej przez grupę mięśni.

URZĄDZENIE POMIAROWE

Stanowisko składa się z następującego elementów:

1. rama mocująca,

2. blok obrotowy,

3. dźwignia,

4. siedzisko,

5. gumy - ekspandory,

6. fotodioda,

7. przetwornik fotoelektryczny,

8. miernik czasu.

WYKONANIE POMIARU

1. Ustabilizować badanego na siedzisku tak, aby oś obrotu stawu kolanowego pokrywała się z osią bloku obrotowego.

2. Do bloku obrotowego założyć odpowiednią liczbę gum o znanej i wywzorcowanej sile naciągu.

3. Badany napędza dźwignię podudziem, prostując je w stawie kolanowym z maksymalną prędkością. Przy każdym obciążeniu wykonać po 2 próby.

4. Zarejestrować czas pokonania ustalonego odcinka drogi kątowej α = 26˚ = 0,454 [rad] i dane pomiarowe wpisać do karty.

5. Wykonać obliczenia prędkości kątowej ω i mocy chwilowej P.

6. Sporządzić wykresy.

OPRACOWANIE WYNIKÓW

1. Zmierzony czas wyprostu (t) kończyny w stawie kolanowym (wynik lepszy z dwóch zmierzonych) został zapisany w tabeli 2. i podany w [ms].

2. Następnie obliczono prędkość ( ω ) prostowania kończyny dla poszczególnych wartości obciążenia wg zależności:

ω	=	α
				t

α = 0,454 rad

3. Moc (Pbzw ) rozwijana przez badanego dla poszczególnych wartości obciążenia została wyliczona ze wzoru: P = ω Mr , gdzie Mr - to stały moment oporujący.

4. Moc względną (Pwz ) obliczono dzieląc wartość mocy bezwzględnej przez masę ciała.

5. Na podstawie otrzymanych wyników opracowano charakterystyki zależności prędkości kątowej (wykres nr 1.), mocy bezwzględnej (wykres nr 2.) i mocy względnej (wykres nr 3.) od wielkości obciążenia (liczba gum).

Wszystkie obliczone wyniki zawarte są w tabeli nr 2.

MATERIAŁ BADAŃ

Badania przeprowadzono na studentach 1 grupy męskiej III roku WF.

Tabela nr 1.

	IMIĘ I NAZWISKO	DYSCYPLINA	MASA CIAŁA	WZROST
1. 2. 3. 4. 5.	Michał Zembrzuski Wojciech Zajkowski Piotr Jaros Marcin Jakubowski Łukasz Heimann	kolarstwo szosowe judo nie trenuje nie trenuje nie trenuje	70 kg 73 kg 85 kg 86 kg 83 kg	180 cm 178 cm 180 cm 178 cm 180 cm

WYNIKI BADAŃ

Tabela nr 2.

LICZBA GUM ------------ wartość obciążenia [Nm]		MICHAŁ ZEMBRZUSKI	WOJCIECH ZAJKOWSKI	PIOTR JAROS	MARCIN JAKUBOWSKI	ŁUKASZ HEIMANN
2 ---------- 18,3	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	40 11,35 207,7 2,97	38 11,95 218,68 2,99	41 11,07 202,58 2,38	38 11,95 218,68 2,54	38 11,95 218,68 2,63
4 ---------- 35,5	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	43 10,59 375,94 5,37	39 11,64 413,22 5,66	44 10,32 366,36 4,31	40 11,35 402,92 4,68	42 10,81 383,75 4,62
6 ---------- 52,7	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	46 9,87 520,15 7,43	46 9,87 520,15 7,12	48 9,46 498,54 5,86	42 10,81 569,69 6,62	46 9,87 520,15 6,27
8 ---------- 69,9	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	50 9,08 634,69 9,07	50 9,08 634,69 8,69	49 9,26 647,27 7,61	44 10,32 721,37 8,39	46 9,87 689,91 8,31
10 ---------- 87,1	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	58 7,83 681,99 9,74	55 8,25 718,57 9,84	54 8,41 732,51 8,62	51 8,9 775,19 9,01	53 8,57 746,45 8,99
12 ---------- 104,3	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	67 6,78 707,15 10,1	60 7,57 789,55 10,81	65 6,98 728,01 8,56	58 7,83 816,67 9,5	55 8,25 860,47 10,37
14 ---------- 121,5	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	80 5,67 688,9 9,84	65 6,98 848,07 11,62	66 6,88 835,92 9,83	67 6,78 823,77 9,58	61 7,44 903,96 10,89
16 ---------- 138,7	t [ms] ω [rad/s] Pbzw. [W] Pwz. [W/kg]	91 4,99 692,11 9,89	77 5,9 818,33 11,21	77 5,9 818,33 9,63	79 5,75 797,52 9,27	72 6,3 873,81 10,53

Wszystkie badane osoby charakteryzują się zbliżonymi wartościami wysokości ciała (tabela nr 1.). Różnica w budowie dotyczy jednak masy ciała. Michał i Wojtek są o ponad 10kg lżejsi od pozostałych. Wszyscy są bardzo aktywni fizycznie jednak Michał i Wojtek zajmują się sportem wyczynowo.

Na wykresie nr 1. przedstawiona została zmiana prędkości kątowej (ω) w zależności od zwiększającego się obciążenia. U wszystkich badanych zauważamy właściwy spadek prędkości po każdorazowym zwiększeniu zakładanej liczby gum. Zmniejszanie prędkości kątowej jest proporcjonalne do zwiększenia obciążenia. Różnice w wynikach są bardzo niewielkie. Najwyższe wartości prędkości można zauważyć u Łukasza, a najmniejszy spadek tej wielkości u Piotrka.




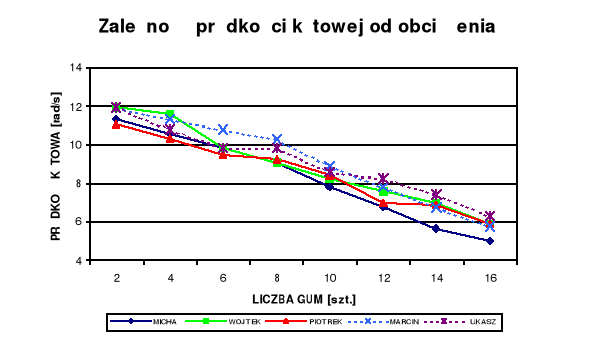
WYKRES nr 1.

Wykres nr 2. ilustruje natomiast zależność mocy chwilowej od zmieniających się wartości obciążenia. Moc wraz ze wzrostem obciążenia rośnie. Zwiększanie mocy przy początkowym obciążeniu jest bardziej gwałtowne, następnie maleje przyrost. U wszystkich badanych zauważamy zmniejszanie mocy przy obciążeniu przekraczającym 100 Nm , czyli po założeniu 12 lub u niektórych 14 gum. Wartości rozwijanej mocy przy najmniejszym obciążeniu są zbliżone. Największe wartości mocy osiąga Łukasz. U Michała zauważyć można najmniejszy przyrost mocy, jednak osiągając wartości ok. 700W moc utrzymuje się na stałym poziomie. U pozostałych badanych przebieg zmian i wielkość wartości mocy jest bardzo zbliżony. Z przebiegu tych zmian można odczytać wielkość obciążenia, przy którym badany osiąga najwyższą moc.

3

---