17498 Image0003

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE - metody numeryczne

Klasyfikacja z uwagi na stopień pochodnych funkcji celu Q (x):

■    algorytmy rzędu zerowego (bezgradientowe),

Korzystają tylko z obliczonych wartości funkcji Q (x).

■    algorytmy rzędu pierwszego (gradientowe),

Korzystają z pierwszych pochodnych funkcji Q(x); (kierunek —\7^rQ (x) przeciwny do gradientu funkcji) jest kierunkiem jej najszybszego spadku).

■    algorytmy rzędu drugiego,

Korzystają z drugich pochodnych funkcji Q (x) lub jej hesjanu H

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE - metody numeryczne

MINIMALIZACJA FUNKCJI JEDNEJ ZMIENNEJ

j k    £+1

Po ustaleniu kierunku poszukiwań a , problem znajdowania kolejnego punktu x sprowadza się do minimalizacji funkcji jednej zmiennej:

znajdź X_k = A_fc takie, że Q(x^A+l ) = <5(x* -j-A^d* ^j = Q ^A^^min    (4.2)

lub po podstawieniu X_f =x, Qf x) —»min =>x — x

ALGORYTMY BEZGRADIENTOWE PODZIAŁU I REDUKCJI ORAZ INTERPOLACJI

Założenie:

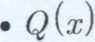
ma ona jedno minimum w punkcie