29400 MATEMATYKA012

16 I Wiadomości wstępne

Dowód. Zgodnie z przyjętymi oznaczeniami mamy:

z,z₂ =|z,|(cos(p₁ -f isin<p,)|z₂|(cos(j>₂ -+• i sin <p₂) =

=|z, ||z₂ |((COS<p, cos(p₂ - sin (p, sin (p₂) +

+i(sin <p, cos(p₂ + cos<p, sin <p,)) = =|z,||Zj|(cos(<p, + <p₂) + isin(<p, + q>₂)).    D

Posługując się metodą indukcji matematycznej można udowodnić analogiczne twierdzenie o iloczynie dowolnej skończonej liczby czynników.

TWIERDZENIE 2.1* Jeżeli z_k =|z_k|(cos<p_k + isin<p_k), k =    , to

z.i-...z„ =|Z|K-*|zJ(cos(<p₁+...+(p_n) + isin((p₁+...+<p_łt)).

TWIERDZENIE 2.2 Jeżeli z, =|z, |(cos<p, 4- i sin cp,), z₂ =|z₂|(cos(p₂ + isin<p₂)*0, to

f =!fi(cos(<p_l--<p,) + isin((j),-<!>,)).

^Z 2 l^Z21

POTĘGOWANIE LICZB ZESPOLONYCH W POSTACI TRYGONOMETRYCZNEJ W zbiorze liczb zespolonych przyjmujemy, tak jak to było w zbiorze liczb rzeczywistych, następującą definicję potęgi o wykładniku naturalnym n: n-tą potęgą liczby zespolonej z nazywamy iloczyn n czynników równych z:

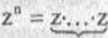
n

Z twierdzenia 2.1' przyjmując z, =... = z_n =- z , otrzymujemy

TWIERDZENIE 2.3 Jeżeli z =|z|(cos<p f i sin <p), lo (2.6)    z" =|z|"(cosn<p + isin n<p), neN.

Z powyższego twierdzenia łatwo otrzymujemy dla każdego <p G R i n g N następujący wzór nazywany wzorem Moivre’a

(co$<p + i sin <p)^B = cosntp + isin mp.

Wzór (2.6) jest szczególnie użyteczny w przypadku gdy liczbę potęgowaną łatwo zapisać w postaci trygonometrycznej, a wykładnik potęgi jest duży. Ilustruje to poniższy przykład.

PRZYKŁAD 2.4 Obliczymy

a) (-1+i)¹⁹,    b)(l+i)^M,    c)(l-iV3)"^s.

Najpierw liczbę potęgowaną zapiszemy w postaci trygonometrycznej, a następnie zastosujemy wzór (2.6).

a)    -1 + i = >/2(cos(3rc/4) + isin(37i/4)),

(-1 + i)” = >/2^l9(cos(57jt/4) + isin(577t/4)) =

= v2 (cos(147i + 7i/4) + isin(147t + 7t/4)) =

= >/2^l9(cos(7c/4) + isin(7i/4)) = 2^v(l + i);

b)    1 + i = >/2(cos<7c/4) -t- i sin(7t/4)),

(1 + i)²⁰⁸ = Si** (cos52tc + i sin 527t) = 2^]0*;

c) l-,V3 = 2(cos(-7c/3) + isin(-7t/3))₁

(1 - i V3)"⁵ = 2^,,s(co$(-1 15tc/3) + i sin(-l 15tc/3)) =

= 2"⁵(cos(387c + n/3)-isin(387c + ;c/3)) =

= 2^,15(cos(7r/3) - i sin (tu/3)) - 2^,,4(1 - i VJ).    ■

Pierwiastkowanie liczb zespolonych w zbiorze liczb rzeczywistych określony jest arytmetyczny pierwiastek stopnia n liczby nicujcmnej. A mianowicie: przy założeniach, że a > 0 i n e N mamy:

(H/a=b) o (b*0 a b'^ł=a).

Zgodnie z tym określeniem = 3, gdyż 32:0 i 3² =9; natomiast

y[9 * -3, gdyż -3 < 0. Definicji takiej nic można przenieść bez zmian na pierwiastki liczb zespolonych choćby dlatego, że nic ma sensu mówić o znaku liczby zespolonej. W zbiorze liczb zespolonych przyjmujemy następującą definicję pierwiastka.

Pierwiastkiem stopnia naturalnego n liczby w nazywamy taką liczbę z, że