MATEMATYKA011

14 I Wiadomości wstępne

Moduł liczby obliczamy zgodnie ze wzorem (2.4), natomiast argument znajdujemy korzystając z interpretacji geometrycznej argumentu (w przypadku a) - c)) lub z definicji, czyli z równań (2.5).

a)    |-4|= 4, arg(-4) = 7t;

b)    |3i|= 3, arg(3i) = tc/2;

c)    |2-2i|= t]2² +(-2)² = 2>/2, arg(2-2i) = -7t/4;

d)    |-l-V3i|=ą/( l)"’+(-V3)^: =2; argument tej liczby wyznaczamy z równań

1

cos<p = —, sm<p =--.

2    2

Jedynym rozwiązaniem tego układu w przedziale (-7C,7C> jest (p₀ =-2tc/3. Zatem arg(-l~V3i) =-2tc/3.    ■

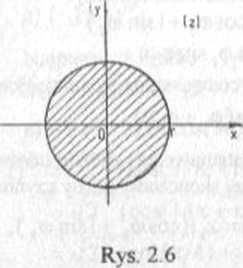
Zgodnie z interpretacją geometryczną modułu liczby zespolonej, zbiór wszystkich punktów' z płaszczyzny zespolonej spełniających warunek

|z|<r, r>0,

jest wnętrzem koła (rys. 2.6) o środku w początku układu i promieniu r, które oznaczamy przez K(0,r) Zatem przy założeniu, że r > 0 mamy

{zeC: |z|<r} = K(0,r).

Moduł różnicy dwu liczb z = x + iy oraz z₀ = x₀ +iy₀ wyraża się w zorem    __

|z - z₀|= yl(x -x₀)^J + (y -y„)^J i jest równy odległości punktów z i z₀. Zatem dla r > 0 {zef: |z-z₀|<r) = K(z₀,r),

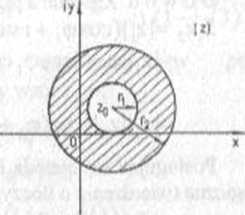
gdzie K(z₀, r) oznacza wnętrze koła o środku w punkcie z₀1 promieniu r. Podobnie dła 0 < r, < r₂ mamy:

{zeC: r,<|z-zj<r,} = P(z₀;r„r_J), gdzie P(z₀,r,,r₂) oznacza wnętrze pierścienia o środku w punkcie z₀ i promieniach r,, r₂ (rys. 2 7).

POSTAĆ TRYGONOMETRYCZNA LICZBY ZESPOLONEJ. Z równości (2.5) otrzymujemy:

x=|z|cos<p, y=|z|sin<p.

W konsekwencji

z = x + iy = |z|cos<p + i|z|sin (p = |z|(coscp + isin<p).

Zatem każdą liczbę zespoloną z różną od zera można zapisać w tzw. postaci trygonometrycznej

z=|z|(cos<p + isin<p),

gdzie |z| oznacza moduł, a <p - dowolny argument liczby z.

Łatwo widać, te dwie liczby zespolone z, =|z, |(cos(p, + i sin q>,) i z₂ =|z₂|(cos<p₂+isin<p₂) są równe jedynie wtedy, gdy ich moduły są równe, a argumenty różnią się o wielokrotność 2k. Zatem

(z, = z₂) o (|z,|=|Zj| a ^p,-<pj = 2ktt).

MNOŻENIE I DZIELENIE LICZB W POSTACI TRYGO-NOMETRYCZNEJ. Niżej podajemy twierdzenia o mnoźcniU i dzieleniu liczb zespolonych w postaci trygonometrycznej:

TWIERDZENIE 2.1 Jeżeli z, =|z,|(c°s<p, + isin <p,), z₂ =|z₂|(cos<p₂ + i sin cp₂), to

Zi*2 =|Z|||Zj|(cos(<p, +<pj) + isin(<p| +<|>₂)).