43200 skan0007 (8)

34

Całkę szczególną równania niejednorodnego wyznaczymy metodą przewidywań. Funkcję f rozbijemy na dwie, tzn. f(x) = fi{x) 4- h{x), gdzie

fi(x)^;p= sin 2x,

mmmm,

i dla każdej z nich odgadniemy całkę szczególną, więc F(x) = Yi(x) 4- ^(a;), gdzie

Yi(a:) = A sin 2x 4- Bcos 2$,    = Ce^5x.

Stąd

Y'{x) ~ 2Acos2x - 2B sin 2x + 5Ce^5x,

więc

2 A cos 2x — 2B sin 2x + 5 Ce^5x + A sin 2x + B cos 2x + Ce^Sx = sin 2x 4- e^5x.

Porównajmy współczynniki przy cos 2x, sin 2x i e⁵*, aby otrzymać układ równań:

2A + B = 0 -2 B + A = 1 6C = 1

cos 2x sin 2a;

„5 a;

Po rozwiązaniu tego układu mamy

a więc całka szczególna ma postać:

1    2    1

Y(*) Mm sin 2x - jcos 2x 4- -e^5x. 5    5    o

Stąd

1 I

y(x) = yo (x) 4- y(a;) = Ce ^x 4- ^ sin 2a: — ^ cos 2a: + -e^5x.

Odp.: y = Ce ^x 4- \ sin 2x — \ cos2a: + he^5x.

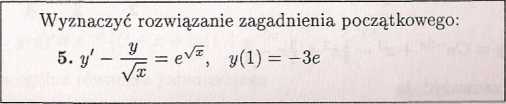
5. Rozwiązujemy najpierw równanie jednorodne

o,

V

^v

M .

Jest to równanie o zmiennych rozdzielonych, a więc

dy _ dx V ~

Całkując je, otrzymamy rozwiązanie ogólne:

Rozwiązanie szczególne równania liniowego niejednorodnego wyznaczymy metodą uzmiennienia stałej, a więc

Y{x) = L(x)e²^.

Obliczamy

v^x

i wstawiamy wyrażenia Y i Y' do równania wyściowego, otrzymując

V* y/x

czyli	stąd L(x) = J e~^dx.
Podstawiamy	yfx = t => x = t^2, stąd dx,4= 2tdt,
a więc	L(x) = 2 J te~*dt.
Całkując przez części, otrzymamy
	L(x) =^—2e ^t(t + 1) + C\ |j§|—2e ^*(y/x + 1) + C\
a stąd	Y{x) = -2e^2^e^{y/x + 1) B-2e^(\/x + 1).

/atom rozwiązanie ogólne danego równania jest opisane wzorem y{x) = y₀(x) + Y(x) = Ce²^ - 2e^(y/x +1).

Uwzględniając warunek początkowy y( 1) = -3e, otrzymamy C. = e^_1. Oclp.j y -    - 2e^(y/x + 1).