73533 S6300991

276

Rozdział 2. Granice funkęj-

1.13    a) S = {-1,1}; b) S = {O, §, l}; c) S = {0,oo>; d) S =

_e) s= {-1,1}; f) S =    8) ^S== t⁰’⁰⁰)’ ^h*) ^S = l°> ¹1-

i*) s = {-5, -3,3,5}; j*) S = [-1,1].

1.14 a) lim a„ = -oo, firn a„ = oo; b) lim b_n = -1, lnn^bn = 1;

c) lim Cr. = -2, Hm Cn = 2; d) lim dn = o, lim d_n = oo; n *oo    n—»oo    «—♦ oo    ⁿ~~*°°

e) Hm in = 1, lim x„ = 3; f) lim y_n = 0, lim y_n = oo;

n—oo_    n—*oo    ⁿ~’°° --

k) lim Zn = -1, lim z„ = 1; h) lim v_n — -oo, ™ v_n = oo;

n^óó    ⁿ-°°    n—.oo    n-~oo

i*) lim tUn — 0.1, lim Wn ⁼ 1; j*) lim tn ⁼ 1» lim tn 9.

n—oo    n—oo    n—oo

Rozdział 2 (str. 88)

, .    6\/3

2.3 a) lim r(x) = 0, lim r(x) = —

x—.0+    *—♦$    ^D

b)    lim x(t) = 5. Wynik ten oznacza, że cząstka wykonując drgania tłumione wzglę. dem punktu xo = 5 zbliża się do niego, gdy t —♦ oo;

c)    lim xi(a) = —4, lim X2(a) = oo, lim xi(a) = 0, lim X2(a) = 0.

_o_,0+    o—>0+    a—»oo    o—»oo

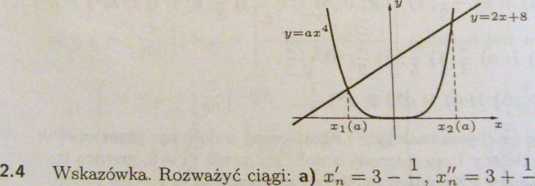
^b) ^x'n - y -4 - -, x" = y4+^; c) x'_n = 2n7r, x'ń = Ę + nir; d) xń = 7T - x'ń = 7T + i; e) x'_n = a/4 — —, x" = tM +

f) x_n — n²7r², x" =    + 2T17A ; g) x'_n = 7r + —, x" = w -

\2    /    n    n

h) x_n = n, xń = n + i) x'_n = ■ -L-, x" = -7===;

x    V 2nłr    v 7r + 2n"jr

j) ^xn — x'ń = —; k) x'_n = 2mr, x'ń =    + 2rwr;

n + 1

n + 1

l)x^/n = 5-_T4-T,x^/ń = 5+    ¹

1

~7S

1

2.5 a) 0; b) nie istnieje, bo lim 2* = 0, lim 2** — 00; c) 2;

X³)]

d) nie istnieje, bo lim r-— = -4, lim _r-rr = 4; e) 0;

*—2- |x — 2|    *_2+ |x - 2|

f) nie istnieje, bo lim sgn jx(l — x²)l = l, lim sgn [x (1

^{L v}    '^J    _x__i+

■MMMM