69681 str305

§ 5. POCHODNE TENSORÓW 305

3. divF = V,^kk =

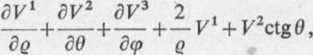
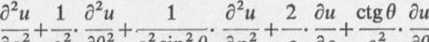
cq q cu g sin i; v(p e    a ^vd

AU =

§ 6. Tensory kartezjańskie

Definicja 1. Transformacją liniową ortogonalną przekształcającą układ współrzędnych z, w układ współrzędnych z_T nazywamy transformację

(6.1)

z_r — A_rsz_s + B_r,

przy czym współczynniki A„ mają następującą własność:

(6.2)

gdzie

(6.3)

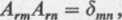
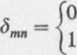
dla    m n,

dla    m = n.

Własność 1. Jeżeli współczynniki A_rs spełniają warunki (6.2), to spełniają one również związki

(6.4)

Własność 2. Współczynniki A_rs występujące w liniowej transformacji ortogonalnej (6.1) czynią zadość następującej relacji:

co wynika z własności (6.2).

Definicja 2. Tensorami kartezjańskimi nazywamy te wielkości, które transformują się według tych samych praw co tensory, ale w przypadku liniowej ortogonalnej transformacji współrzędnych (6.1).

Własność 3. Każdy tensor jest tensorem kartezjańskim, ale nie każdy tensor kartezjański jest tensorem.

Własność 4. Prawo transformacyjne tensorów kartezjańskich nie zmienia się na skutek podniesienia lub obniżenia wskaźnika.

Własność 5. W przypadku tensorów kartezjańskich nie występuje różnica pomiędzy składowymi kowariantnymi i kontrawariantnymi.

Uwaga. W przypadku tensorów kartezjańskich wszystkie wskaźniki będziemy pisali zawsze na dole. W tym rozdziale będziemy zajmowali się tylko układami współrzędnych kartezjańskich ortogonalnych, a zatem wszelkie transformacje współrzędnych będą zachodziły według relacji (6.1) i nie ma potrzeby odróżniania tensorów kontrawariantnych

20 — Wybrane działy matematyki...