79257 Scan0043

54 Iloczyn kartezjański. Relacje

5.3.1 Relacje binarne

Definicja 5.4 Relacją binarną nazywamy związek między elementami x i y par uporządkowanych (x,y), gdzie x £ X i y E Y, co zapisujemy

xpy

i czytamy ”x pozostaje w relacji p z y”.

Relacja jest podzbiorem iloczynu kartezjafiskiego, tzn. można określić zbiór

R = {(x,y) : xpy} C X x Y

zwany wykresem relacji. Mówimy wówczas, że relacja p jest określona w iloczynie X x Y.

Uwaga 5.2 W praktyce zbiór R utożsamia się z relacją p i mówi się, że ”x pozostaje w relacji R z y ”.

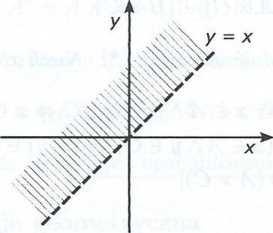
Przykład 5.5 Wykresem podanej relacji jest pólplaszczyzna położona nad prostą x = y bez tej prostej.

R = {(x,y) € M² : x < y}

Definicja 5.5 Dziedziną D (R) relacji nazywamy zbiór poprzedników par (x,y) należących do tej relacji:

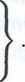
D (R) = <x £ X : \J xRy

[    yer