82070 instalacje110

4. TEORIA SILNIKÓW SKOKOWYCH 102

średni moment obrotowy zaś

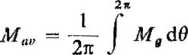
o

(4.12)

Założono, że rezystancja i indukcyjność poszczególnych pasm są identyczne, co zazwyczaj występuje w praktyce. Ponadto w modelu założono zmienność indukcyjności pasma jako kosinusoidalną funkcję kąta 0, co jest do przyjęcia dla silników, w których stosunek szerokości zęba do grubości szczeliny powietrznej jest mniejszy niż 20.

Model matematyczny silnika skokowego o magnesie trwałym na wirnika

Jedną z podstawowych prac dotyczących dynamiki silnika skokowego o magnesach trwałych umieszczonych na wirniku jest publikacja D.J. Robinsona i C.K. Tafta [91], w której rozpatrzono zlinearyzowany model matematyczny tego silnika, analizowany w zakresie jednego skoku. Jakkolwiek autorzy nazywają swój model — modelem silnika skokowego o magnesach trwałych, to w świetle dzisiejszych pojęć, rozpatrywany silnik zaliczylibyśmy do grupy hybrydowych, gdyż opisany silnik ma na wirniku magnes trwały namagnesowany poosiowo i dwa uzębione pakiety

n₂(t)

R

W1 urft)

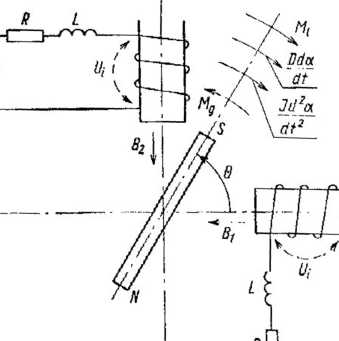
Rys. 4.6. Schemat modelu silnika skokowego o magnesach trwałych na wirniku

z miękkiej magnetycznie stali po obu jego stronach, tak jak silnik pokazany na rys. 2.20a. W czasie kiedy była publikowana praca [91] nie posługiwano się jeszcze powszechnie pojęciem silnika hybrydowego.

Rysunek 4.6 przedstawia schemat modelu matematycznego silnika skokowego o magnesach trwałych wg [91]. Równania napięć doprowadzonych do pasm uzwojenia silnika mają postać

«,(') - «h(<)+L    + U,    (4.13)

(4.14)

Napięcie indukowane U_t jest generowane w pasmach uzwojenia stojana dzięki ruchowi wirnika z magnesem trwałym w stosunku do biegunów magnetycznych stojana. Zakładając sinusoidalny rozkład indukcji magnetycznej stojana i posługując się równaniami Maxwella, napięcie indukowane można wyrazić wzorem

(4.15)

_rr K_e d0(/) .

gdzie:

K_e — stała wiążąca napięcie indukowane i indukcję magnetyczną stojana, V-s/stopieó;

Z_r — liczba zębów wirnika.

Po uwzględnieniu zależności (4.15) równania różniczkowe napięć pasm uzwojenia stojana przyjmą postać

«ł(r) = Rii(t) +L

dt

*e

Zr

dfl(r)

dt

sin 0 (t)

(4.16)

«j(0 = Ri_x(,) ~ + A <«(') _cos    (4.17)

Moment obrotowy wytwarzany przez silnik skokowy przy obu pasmach zasilonych może być wyrażony — w zależności od indukcji magnetycznej B w stojanie i momentu magnetycznego H wirnika — równaniem

(4.18)

M₉ = B_z IIcos 0 (t) - B_t Hsin 6 (/) w którym H — moment magnetyczny wirnika, A/m.