33104 instalacje111

4. TEORIA SILNIKÓW SKOKOWYCH 104

Moment magnetyczny wirnika jest funkcją jego geometrii i energii zastosowanego magnesu trwałego. Indukcja magnetyczna jest proporcjonalna do liczby zwojów uzwojenia stojana oraz prądu i(t) w uzwojeniu. Zatem wytwarzany moment obrotowy może być wyrażony jako

(4.19)

M_g = Km h(0 ^{cos 0} (0 - K_m i iii) sin 6 (/)

gdzie K_m — stała momentowa, W/A.

Momentowi M_g generowanemu przez silnik przeciwstawiają się działające na wale, przeciwnie skierowane, mechaniczne momenty składowe:

— moment spowodowany bezwładnością wirnika i obciążenia na wale

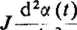
d/* "

— moment tłumienia za pomocą tarcia lepkiego, uwzględniający tłumienie silnika i cieczy tłumiącej,

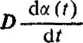
— moment tarcia Coulomba da {t)jdt ^tT |da(0/d/|

— zewnętrzny moment obciążenia na wale

M^i)

przy czym między kątem 0 i kątem obrotu a zachodzi relacja 6 = Z_r a

Przyrównując mechaniczne momenty oporu na walc do momentu generowanego przez silnik skokowy, otrzymuje się

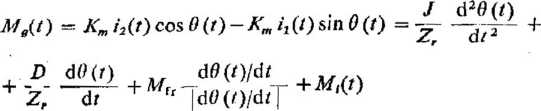
(4.20)

Rozpatrzmy trantmitancję analizowanego silnika skokowego dla punktu pracy, kiedy wirnik jest w równowadze po wykonaniu skoku, przy zasilonych obu pasmach. Wybór tego punktu jest uzasadniony łatwością eksperymentalnego określenia parametrów dla niego. Jako warunki

początkowe przyjęto prędkość i przyspieszenie równe zeru. Uwzględniając warunki początkowe i pomijając tarcie suche, zlinearyzowane równania odnoszące się do tego punktu pracy przyjmują postać

~K_m h-o sin 6₀ A6 (t) -K_m /₂_₀ cos 0_o A0 (?) +K_m cos 0_o Ai₂(t) -

mano

sin ą, A?j(?) = A0(0 + — A° (?) +AA/,(?)
	(4.21)
«i(0 = TJAi^r) +L -i A*4(?) + sin 0O A0 (?)	(4.22)
«i(t) = *A/2(r) +£ -i A;2(r) + cos A0 (/)	(4.23)
Dzięki transformacji Laplace’a równań (2.41), (4.22) i	(4.23) otrzy-
cos A/2(,) - sin AJt(s) - AM,(s) ' ^ I«^2 Ele	(4.24)

~Z--Ź~    ^sln + K_mI2-o cos 0_o

	A£f2(j) + —^ - Ij- cos 90 sAO (s) s Z.T	(4.25)
	R + JLs
	U,(s)+ ^U---- - 1' sin0osA0(s)
/i(*) =	R + Ls	(4.26)

Przez powiązanie równań (4.24), (4.25) i (4.26), otrzymuje się wyrażenie na odpowiedź silnika skokowego w zakresie jednego skoku, przy obu uzwojeniach zasilonych

K,„ cos 6,

i

Jl+Ls I ^AU*(^s) ⁺

A8(s) = -

* J

R_m sin 9,

R +Ls

KukT

A£/,(.t)+

z7 ⁺ X ⁺    (^cos2°»-^sin2(,.)^+

+^_mA-o sin 0_t,+A_m/₂__ocos^

(4.27)