86605 P1111264

54 VHI. Funkcja pierwotna (całka nieoznaczona)

Niech będzie dany ułamek właściwy PIQ, o którym zakładamy, że jest nieskracalny i że jego mianownik Q jest rozłożony na czynniki pierwsze [patrz (3)]. Wówczas całka tego ułamka zapisze się w postaci sumy całek ułamków postaci (5) [lub (6). Jeśli k (lub m) jest większe od jedności, to całki wszystkich ułamków grupy (5) lub (6)] oprócz pierwszej przekształcą się według wzoru (7) pub (8)]. Łącząc wszystkie te wyniki otrzymujemy o-stateczny wzór w postaci

54 VHI. Funkcja pierwotna (całka nieoznaczona)

Część wymierną całki P\IQ\ otrzymujemy w wyniku dodawania wydzielonych wyżej części wymiernych, jest więc ona przede wszystkim ułamkiem właściwym, a jej mianownik Qi ma rozkład

Q_t(x) = (x—a)^k~¹... (x²+px+q)^m~¹

Co się zaś tyczy ułamka P₂/Q₂, który pozostał pod znakiem całki, to otrzymuje się go z dodawania ułamków postaci I i III, a więc jest on również ułamkiem właściwym

Wm h (*-«) — (x²+px+q) ...

Oczywiście [patrz (3)] Q — Q_x Q₂.

Wzór (9) nazywa się wzorem Ostrogradskiego.

Różniczkując można przedstawić go w postaci równoważnej

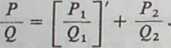
(10)

Widzieliśmy, że wielomiany <2i i Qz można łatwo znaleźć, jeśli znamy rozkład (3) wielomianu Q. Mogą być one jednak wyznaczone również bez tego rozkładu. Rzeczywiście, ponieważ pochodna Q’ zawiera wszystkie czynniki pierwsze, na które rozkłada się Q w potędze o jeden niższej, Q_x jest największym wspólnym dzielnikiem Q i Q\ a więc można go obliczyć z tych wielomianów na przykład przez kolejne dzielenie (czyli za pomocą algorytmu Euklidesa, przyp. tłum). Jeśli znamy £i> to Q₂ wyznaczamy dzieląc po prostu Q przez Q_v

Zajmiemy się teraz wyznaczeniem dzielników P_x i P₂ we wzorze (10). Skorzystamy w tym celu także z metody współczynników nieoznaczonych.

Oznaczmy stopnie wielomianów Q_t Q_u Q_z odpowiednio przez «, n_u n₂, wówczas, n_x+n₂ — n. Stopnie wielomianów P, P_u P₂ nie przewyższają odpowiednio n—1, n_i — 1, 1. Podstawmy za P_x i P₂ wielomiany stopnia /i₄ — 1 i n₂— 1 o współczynnikach literowych. Współczynników tych będzie razem n_t+n₂, tzn. n. Zróżniczkujmy (10) obustronnie, otrzymujemy

P\ Qi-Pt Q'i ,P2__sm^p " Q1 ⁺ Qz Q *

Wykażemy teraz, że pierwszy ułamek można zawsze sprowadzić do mianownika Q w ten sposób, aby licznik pozostał wielomianem. Istotnie,

p' o -P O¹

Pi (U-Pi Qi I ^{1    1} Qi _ Pt Qi-Pi H

5!    Qi 0.2    Q

gdzie H oznacza iloraz Q\ Q₂IQi- Iloraz ten można jednak przedstawić w postaci wielomianu. Rzeczywiście, jeśli (x—a)^k przy k > 1 wchodzi w skład Q_x, to (x—a¥~^l wchodzi, do Q\, a x—a do Q₂. Do takiego samego wniosku dojdziemy, gdy chodzi o wielomian kształtu (x² +px+q)^m dla m > 1. Tak więc licznik ułamka H dzieli się bez reszty przez mianownik, można zatem dalej traktować //jako wielomian stopnia n₂— 1.

Uwalniając się od wspólnego mianownika Q otrzymujemy tożsamość dwóch wielomianów stopnia n—1:

Pi Q₂-P₂ H+P₂ Qi = P.

Jak i wyżej otrzymujemy stąd dla wyznaczenia wprowadzonych n nieoznaczonych współczynników układ n równań liniowych.

Ponieważ możliwość rozkładu (10) została udowodniona dla dowolnego P, więc wspomniany układ musi być niesprzeczny przy wszelkich wyrazach wolnych. Stąd już samo przez się wynika, że wyznacznik układu musi być różny od zera, a więc układ jest oznaczony i rozkład (10) jest określony dla danych mianowników Qi i Q₂ — jednoznacznie (¹).

Przykład. Wydzielić część wymierną całki

dx.

f 4x⁴+4x³+16x²+12x+8

(x+l)²(x²+l)²

Mamy

Gi = ea = (¹+1)(¹²+1)

4x⁴+4x³ + 16x² + 12x+8 (x³+x²+x+l)²

₌ [ ax²+bx+c ] l x³+x²+x+l J

x³+x²+x+l,

dx²+ex+f

+

x³+x²+x+l

skąd

4x⁴+4x³ + 16x²+12x+8 =

=(2ax+b) (x²+x²+x+l)—(ax²+6x+c)(3x²+2x+l)+(<ćc²+ex+/)(x³+x²+x+l).

Przyrównując współczynniki przy jednakowych potęgach x z obu stron równości otrzymujemy układ równań, z którego wyznaczymy niewiadome a, b, ...,/:

x⁵ d = 0 (dalej d nie bierzemy już pod uwagę),

x⁴ —a+e = 4,

x³ -2ó+e+/“4,

x² a—b—3c+e+f=¹ 16,

x^l 2a—2c+¹+/« 12,

x° b—c+f= 8,

skąd

1,

1,

c = —4.

0.

3, /“ 3.

na ułamki proste str. 32.

3*

1

Porównaj analogiczną uwagę dotyczącą rozkładu ułamka właściwego